PE 7023 Advanced Production Design

PE 7023 Advanced Production Design

Homework Assignment #1

Single-phase Liquid Inflow Performance Relationship (IPR) is given with the following equation:

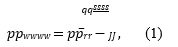
where, 𝑝𝑝̅𝑟𝑟 is the average reservoir pressure, 𝑝𝑝𝑤𝑤𝑤𝑤 is the bottom-hole flowing pressure, 𝑞𝑞𝑠𝑠𝑠𝑠 is the liquid flow rate at standard conditions, and 𝐽𝐽 is the productivity index.

Single-phase Liquid Outflow Performance Relationship (OPR) is given below for vertical upward flow assuming an incompressible liquid and constant friction factor, 𝑓𝑓.

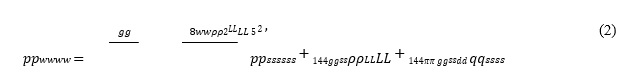
where, 𝑝𝑝𝑠𝑠𝑠𝑠𝑠𝑠 is the separator pressure, 𝑝𝑝𝑤𝑤𝑤𝑤 is the bottom-hole flowing pressure, 𝑞𝑞𝑠𝑠𝑠𝑠 is the liquid flow rate at standard conditions, 𝑔𝑔 is the acceleration gravity of Earth, 𝑔𝑔𝑠𝑠 is the unit conversion factor, 𝐿𝐿 is the depth of the well, 𝜌𝜌𝐿𝐿 is the density of the liquid and 𝑑𝑑 is the diameter of the tubing. Grouping the constant parameters, Eq. 2 can be written as

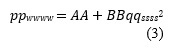
Question:

1. Perform nodal analysis and find the solution point using the following input data:

   𝑝𝑝𝑠𝑠𝑠𝑠𝑠𝑠	100	psig
   𝑝𝑝𝑟𝑟	5000	psig
   𝐽𝐽	5	bbl/D/psi
   𝐴𝐴𝐴𝐴𝐴𝐴	25	o
   𝐿𝐿	8000	ft
   𝑓𝑓𝑀𝑀𝑀𝑀𝑀𝑀𝑑𝑑𝑀𝑀	0.02	-
   𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑔𝑔 𝐴𝐴𝐼𝐼	2.5	in

   1. Plot nodal analysis plot taking bottom hole as the node
   2. Plot nodal analysis plot taking wellhead as the node (Hint: rewrite Equations (1) and (2) for wellhead pressure 𝑝𝑝𝑤𝑤ℎ)
2. Develop an analytical expression for the stability of the Nodal Analysis Equilibrium Solution applying new stability analysis.
3. Write a computer code using a programming language of your choice to determine if the solution is stable or unstable
4. Run your computer code to check for stability:
   1. By varying J and keeping B constant (Arbitrarily define the range for J)
   2. By varying B and keeping J constant (Arbitrarily define the range for B. You can change any parameter included in the definition of B to have a meaningful B range)
5. Present your stability results on a J vs. B (or variable of your choice included in the definition of B) map
6. Discuss your results. What do you see? Please provide your interpretation.

• USA Universities

  • Alabama State University [ASU]
  • Auburn University Montgomery [AUM]
  • Bob Jones University [BJU]
  • Brigham young University [BYU]
  • Brown University [Brown]
  • California State University, Chico [Chico State]
  • Campsbell University assignment help
  • Carnegie Mellon University [CMU]
  • Colorado State University
  • Columbia University [CU]
  • Christopher Newport University [CNU]
  • Denison University [DU]
  • Drew University
  • Florida Atlantic University Navitas
  • Full Sail University
  • George Mason University [MASON]
  • Harrisburg University
  • Hampton University [HU]
  • Hofstra University
  • Howard University [HU]
  • Hult International Business School
  • Illinois State University
  • Johns Hopkins University [JHU]
  • Jackson State University
  • Liberty University assignment help
  • Marshall University
  • New York Institute of Technology
  • New York University [NYU]
  • Northwestern University [NW]
  • Oregon State University
  • Princeton University [PU]
  • Richard Bland College of William and Mary
  • Santa Clara University [SCU]
  • Saint Leo University
  • Stanford Essay help
  • SUNY Geneseo University
  • University of Alabama at Birmingham
  • University of Massachusetts Boston
  • University of California, Berkeley [UC Berkeley]
  • University of California, Davis [UC Davis]
  • University of Florida [UF]
  • University of Georgia [UGA]
  • University of Idaho Navitas
  • University of Maryland, Baltimore County [UMBC]
  • University of Massachusetts Dartmouth Navitas
  • University of Massachusetts Lowell Navitas
  • University of New Hampshire Navitas
  • University of Richmond [UR]
  • University of Rochester [UR]
  • University of Texas [UT]
  • University of South Florida
  • University of Vermont [UVM]
  • University of Virginia [UVA]
  • University of Washington [UDub]
  • Virginia Commonwealth University [VCU]
  • Wake Forest University [WFU]
  • Washington State University
  • Western Washington University [Western]
  • Youngstown State University [YSU]
  • Yale University

  USA Universities Question

  • CS 5480/6480: Computer Networks
  • IT Infrastructure Project Phase II Instructions
  • MCU-CS500: Advanced Data Analysis
  • Purdue University essay Writing
  • GEOL 591 Subsurface Methods
  • PE 7023 Advanced Production Design
  • Econ 201 Principles of Microeconomics
  • NUR 6307 Advanced Nursing Technologies
  • IS 333A Business Computer Systems Analysis