HOME

Multiple Regression Analysis: Estimation and Inference

A consumer organization wants to develop a regression model to predict mileage (as measured by miles per gallon) based on the horsepower of the car’s engine and the weight of the car (in pounds). Data were collected from a sample of 50 recent car models, and the results are organized and stored in Auto.

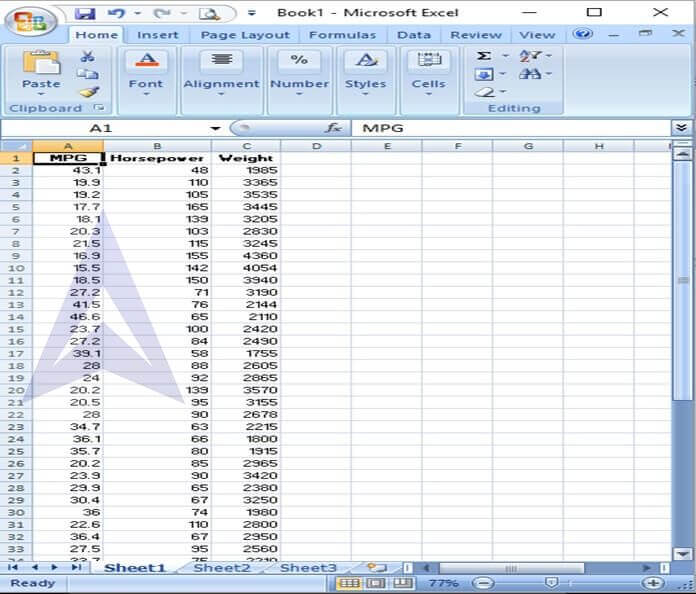
Step 1: Copy the data from the word file and paste it into an Excel worksheet.

MPG Horsepower Weight
43.1 48 1995
19.9 110 3365
19.2 105 3535
17.7 165 3445
18.1 139 3205
20.3 103 2830
21.5 115 3245
16.9 155 4360
15.5 142 4054
18.5 150 3940
27.2 71 3190
41.5 76 2144
46.6 65 2110
23.7 100 2420
27.2 84 2490
39.1 58 1755
28 88 2605
24 92 2865
20.2 139 3570
20.5 95 3155
28 90 2678
34.7 63 2215
36.1 66 1800
35.7 80 1915
20.2 85 2965
23.9 90 3420
29.9 65 2380
30.4 67 3250
36 74 1980
22.6 110 2800
36.4 67 2950
27.5 95 2560
33.7 75 2210
44.6 67 1850
32.9 100 2615
38 67 1965
24.2 120 2930
38.1 60 1968
39.4 70 2070
25.4 116 2900
31.3 75 2542
34.1 68 1985
34 88 2395
31 82 2720
27.4 80 2670
22.3 88 2890
28 79 2625
17.6 85 3465
34.4 65 3465
20.6 105 3380
estimation and inference image 1

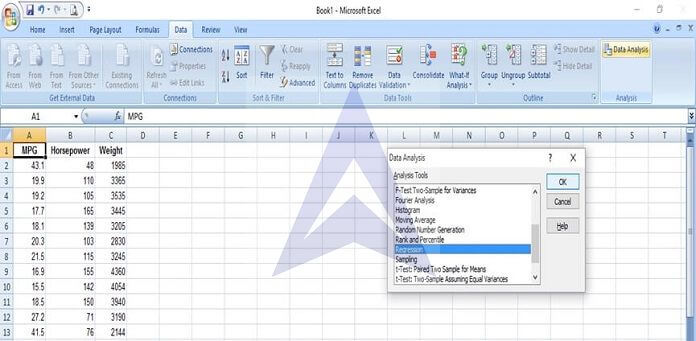
Step 2: Go to the Data thread and select the option – Data Analysis. From the data analysis dialog box, select the option – Regression.

estimation and inference image 2

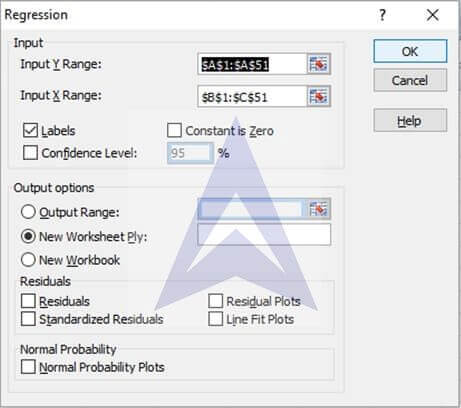
Step 3: select cells A1 to A51 in the input y range and cells B1 to C51 in the input x range. Select the option of labels and set the confidence level at 95%. Select ‘New Worksheet Ply’ from the Output options. Click on Ok. The regression output will instantly display in a new worksheet.

estimation and inference image 3
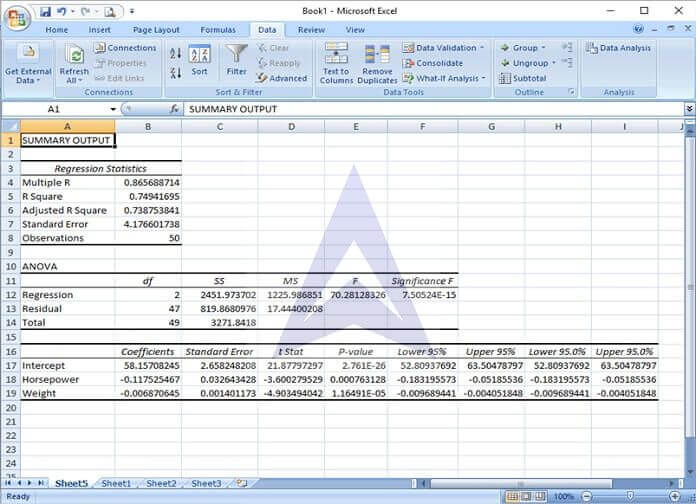
estimation and inference image 4

A. State the multiple regression equation

From the coefficients provided in the regression results, the regression equation is: MPG = 58.16 – 0.11 b1– 0.007 b2

Here, b0 = intercept
b1 = Horsepower of engine
b2 = Weight

B. Interpret the meaning of the slopes, b¹ and b² in this problem

The slope b1 shows that with an increase of 1 horsepower in the engine, the mileage of the car decreases by 0.11 miles per gallon and vice versa.

The slope b2 shows that with an increase of 1 pound in the cars weight, its mileage will fall by 0.007 miles per gallon and vice versa.

Thus, it can be concluded that both, the horsepower of the car’s engine and the weight of the car are inversely related to its mileage.

C. Explain why the regression coefficient, bº, has no practical meaning in the context of this problem

The intercept b0 has no practical implication as the miles that a car will travel will not have a fixed minimum level beyond which it will depend on the horsepower of the engine and the car weight. This statement does not have any practical basis.

D. Predict the mile per gallon for cars that have 60 horsepower and weigh 2,000 pounds

b1 = 60
b^2 = 2000
Hence, the miles per gallon (MPG) will be:
MPG= 58.16 – (0.11*60) – (0.007*2000) = 37.56
Therefore, the miles per gallon will be 37.56

E. Construct a 95% confidence interval estimate for the mean miles per gallon for cars that have 60 horsepower and weigh 2,000 pounds

The confidence interval will be:
Y = MPG ± tn-2,α/2 *sMPG
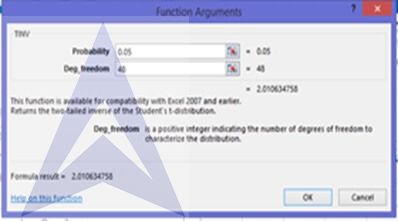
 To calculatetn-2,α/2, select the TINV function in Excel (Formulas -> More Functions -> Statistical -> TINV)
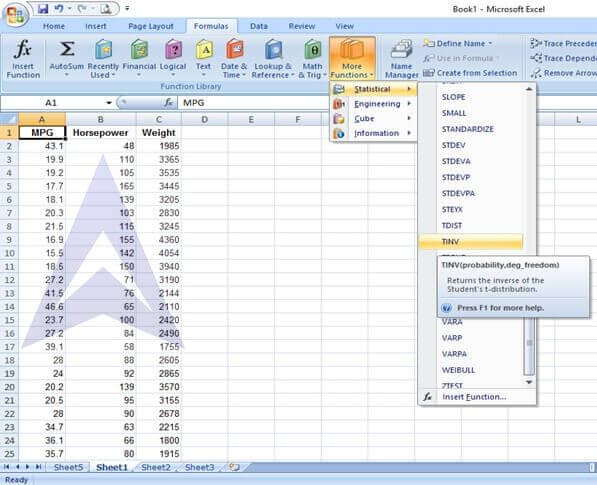
estimation and inference image 5

In the TINV dialog box,

estimation and inference image 6
Thus, we get the value of tα/2 as 2.01
sMPG = 4.176 (from the regression results)
Confidence interval = 37.56 ± (2.01*4.176) = (29.16, 45.95)

F. Construct a 95% prediction interval for the miles per gallon for an individual car that has 60 horsepower and weighs 2,000 pounds

The prediction interval will be:
Y = MPG ± t48,0.05*√sMPG2 + MSE
MSE = 17.44 (from the regression results)
Y = 37.56 ± (2.01*√4.1762+17.44) = (25.70, 49.30)

Write My Essay Services