Excel Tutorial for Normal Distributions
In this tutorial, we will discuss how we can use Microsoft Excel Program to solve questions based on Normal Distributions in statistics and applied statistics and research areas such as econometrics. Normal Distribution refers to a function that represents the distribution of many random variables as a symmetrical bell-shaped graph. In this tutorial of Ms-Excel for Normal Distributions we will learn the following major ways in which we can use the Microsoft Excel program to make calculations related to Normal Distributions:
- Use the NORMDIST function for a probability between 0 and a value x
- Use the NORMDIST function for a probability that is above the x value.
- Use the NORMDIST function looking for the probability between two x values.
- Use the NORMINV
CASE-I
How to Use the NORMDIST function when you are looking for a probability between 0 and a value x (below the x value).
A normal distribution with a mean of 15, a standard deviation of 3, and you are looking for the probability of less than 10.
Use the NORMDIST function
Here is the stepwise procedure on using NORMDIST FUNCTION in EXCEL or area between 0 and the random variable X under the normal distribution curve
Step 1 – Formulas > More functions > Statistical > NORMDIST
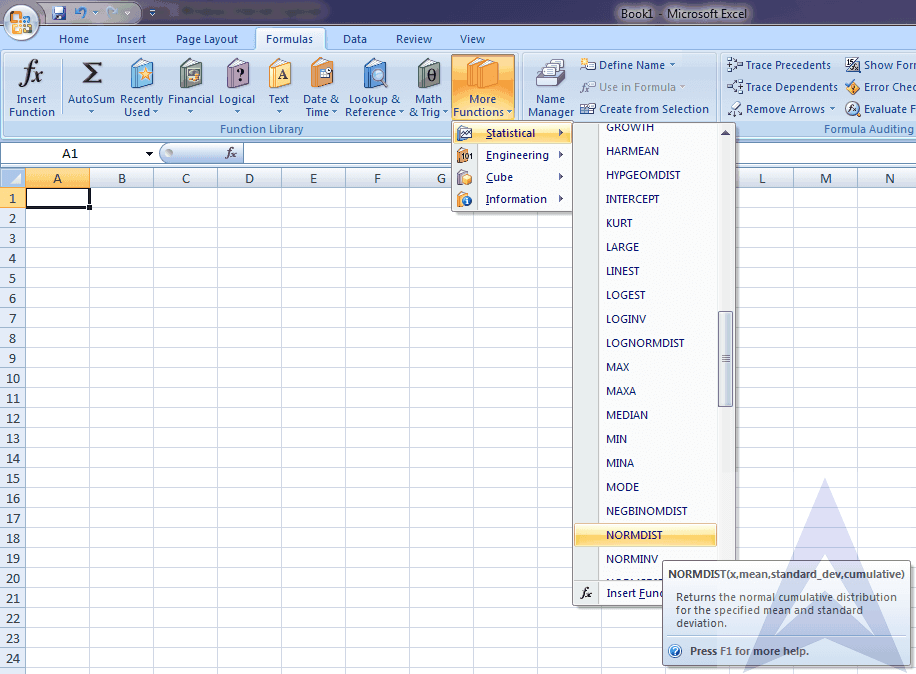
Step 2 – Put the values in functional argument
(cumulative is taken as 1 because we have to find the probability of less than 10) Press OK
And you will get the required value, which here is 0.04779
CASE-II
How to Use the NORMDIST function when you are looking for a probability that is above the x value.
A normal distribution with a mean of 15, a standard deviation of 3, and you are looking for the probability of more than 17.
Use the NORMDIST function
Here is the stepwise procedure on using NORMDIST FUNCTION in EXCEL for finding the probability of being more than X or area to the right of a random variable.
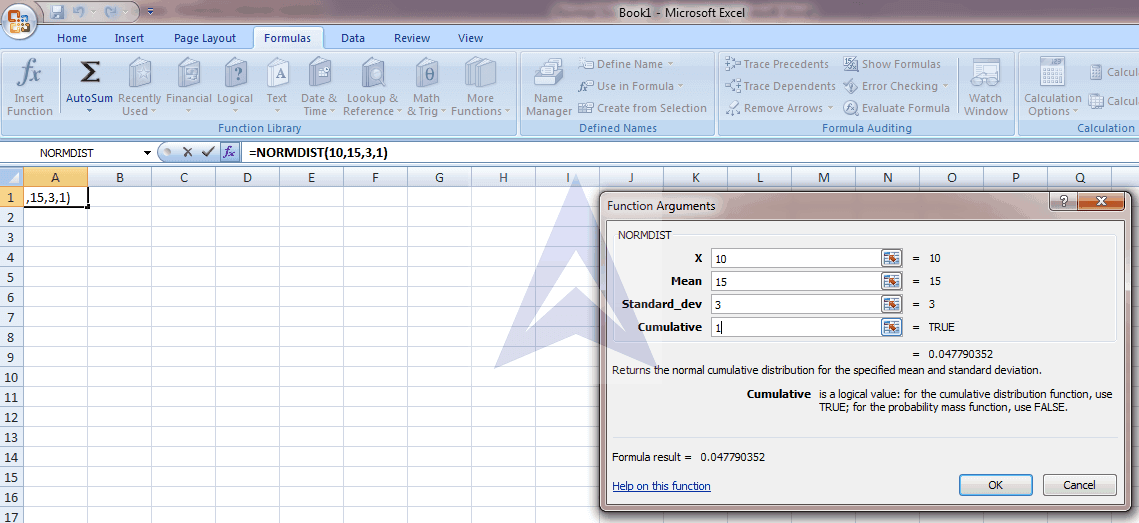
Step 1- Formulas > More functions > Statistical > NORMDIST

Step 2 - Put the values in functional argument. Press OK and you will get the value here as 0.747507
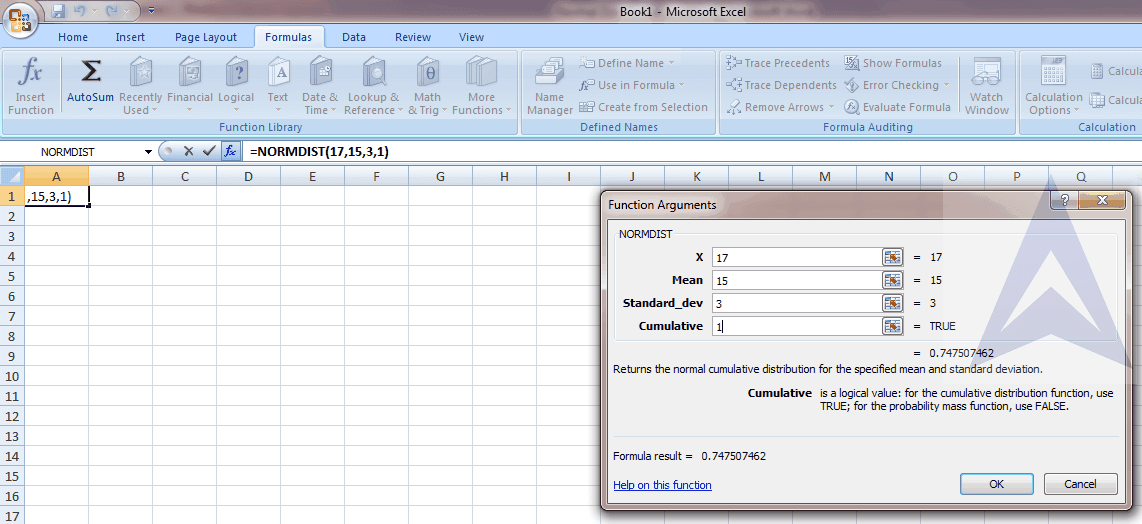
Step 3 - Subtract the above value from 1 and you will get the required answer. For example, here it will be 1- 0.747507 = 0.252493
CASE-III
How to use the NORMDIST function when you are looking for the probability between two x values.
A normal distribution with a mean of 15, a standard deviation of 3, and you are looking for the probability of being between 13 and 16.
Here is the stepwise procedure on using NORMDIST FUNCTION in EXCEL for finding the probability or area under the curve between two random variables.
Step 1 - Formulas > More functions > Statistical > NORMDIST

Step 2 - In this question we have to subtract the value of Probability X less than 13 from Probability X less than 16.
So, calculate the probability of X less than 13 first.
To calculate this Put the values in functional argument. Press OK and you will get the probability of X less than 13 which is 0.252493
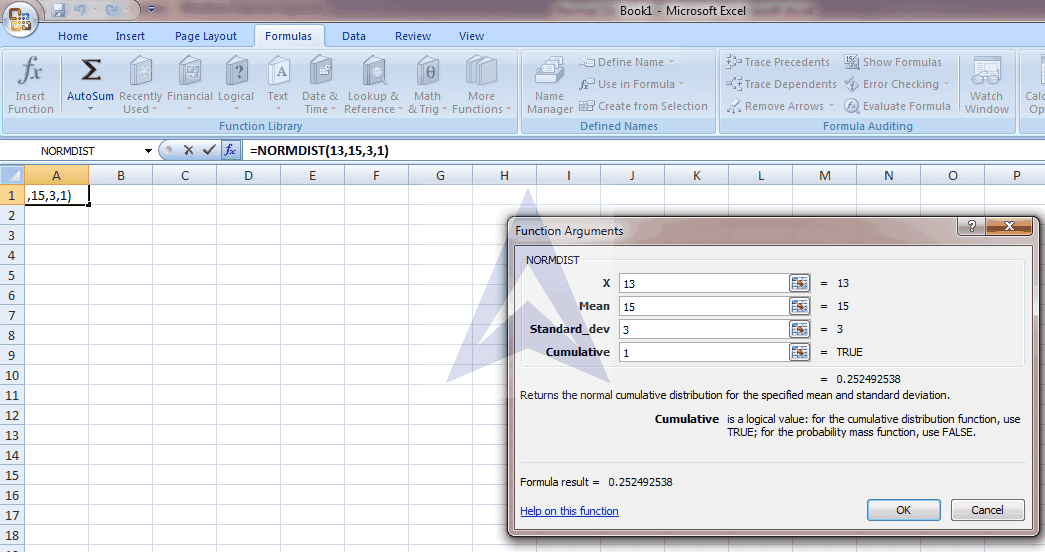
Step 3 - Similarly we calculate the probability of X less than 16 which comes to be 0.630559
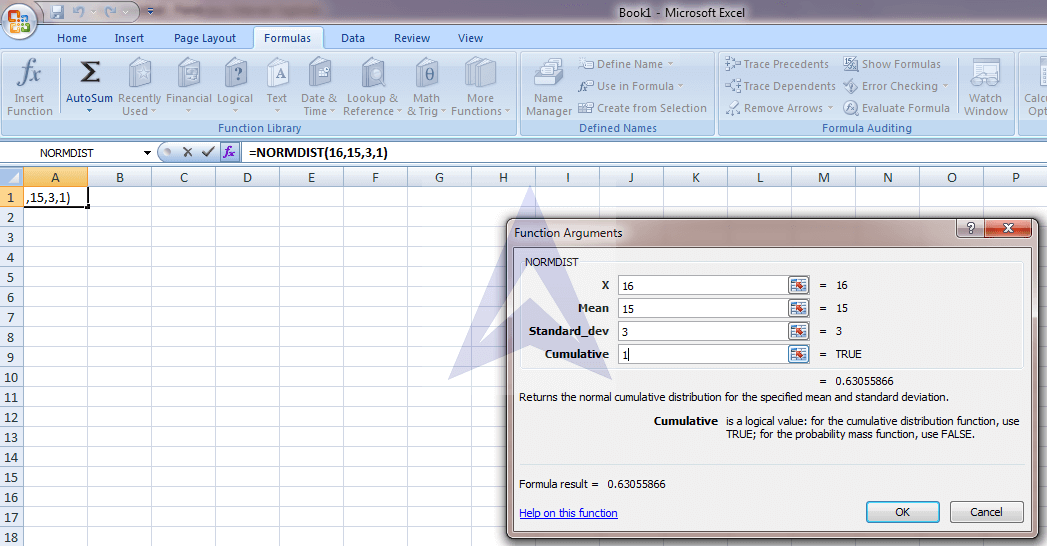
Step 4 – Subtract the probability of X less than 13 from probability of X less than 16 to get the required answer, that is 0.630559 – 0.252495 = 0.378066
So, between 13 and 16 the area under the normal distribution curve is 37.81%
CASE-IV
For a sample of 20, find the probability of less than 14 when you have a normal distribution with a mean of 15 and a standard deviation of 3.
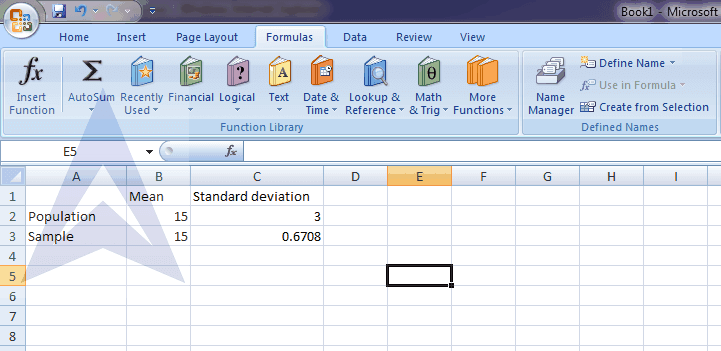
Now you can use the NORMDIST function as given below but we will also have to find the standard error using the formula with standard deviation:
Step 1 - Formulas > More functions > Statistical > NORMDIST

Step 2 - Here sample mean follows normal distribution, with mean = 15, and standard error = standard deviation /√ n i.e. 3/ √20 equals to 0.6708
standard error=σ/√n
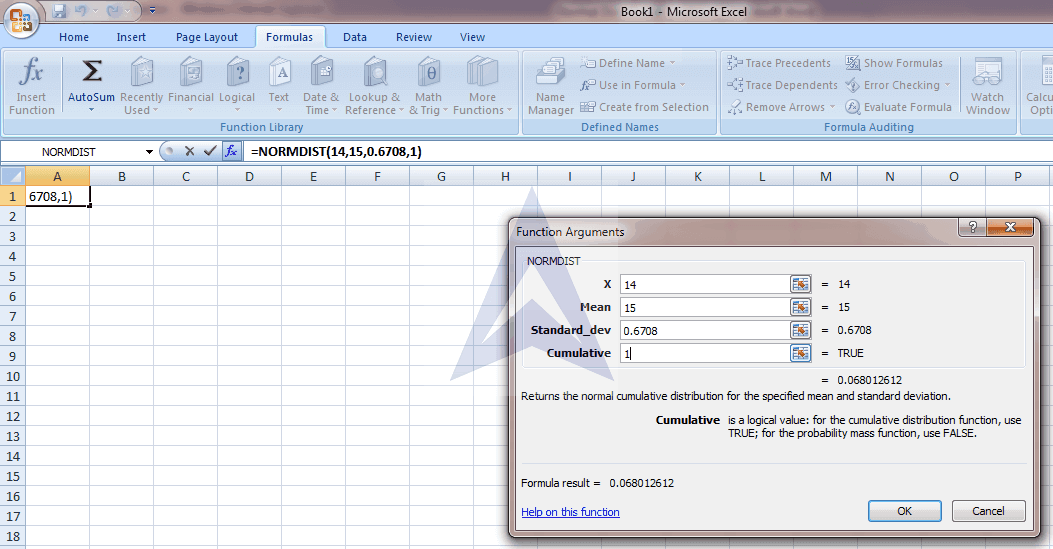
Step 3 - Put the values in functional argument. Press OK and you will get the value of probability X less than 14 that is 0.068013
CASE-V
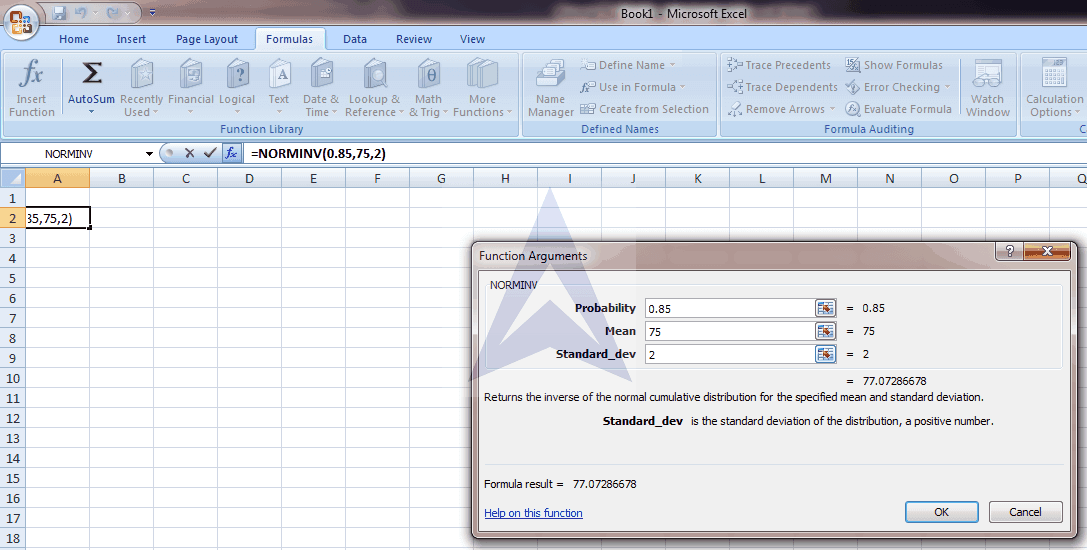
Using the NORMINV function in Excel
A prospective employee is required to take a test. In order to be hired, an employee must score in the top 15%. If the average score on the test is 75 with a standard deviation of 2, what is the minimum score needed to be hired?
For this problem, we use the NORMINV function in Excel. We must also determine if we are looking for a probability that is above the mean or below the mean.
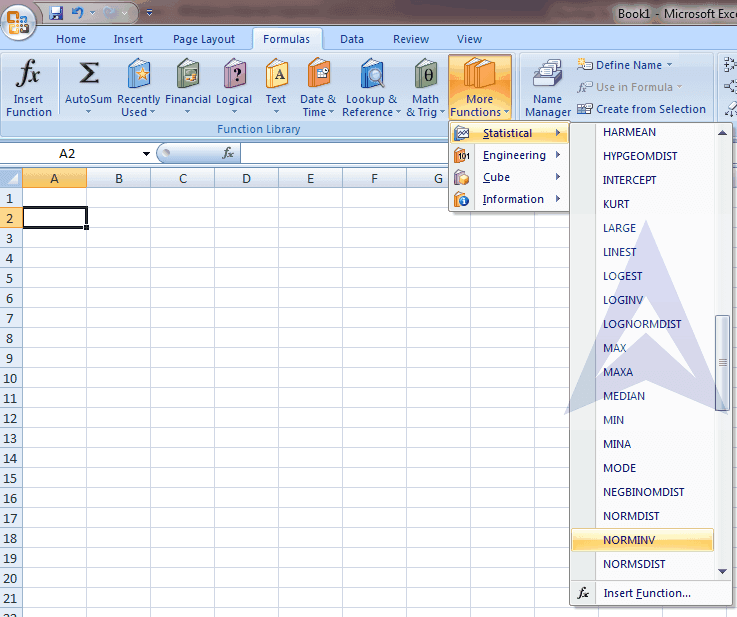
Here is how to use the NORMINV function in excel.
Step 1- Formulas > More functions > Statistical > NORMINV
Step 2 – We have probability of at-most in NORMINV formula. So, we convert the probability as 1- 0.15 = 0.85 and put this value in functional argument and we get the required answer equals 77.07
Looking for help with Probability distributions - Normal, Binomial, Poisson, Hypergeometric etc., find online statistics tutors to help you with probability distribution homework problems, whether you need to do them manually or using statistical software such as SPSS, STATA, Eviews, Excel, Python or R programming.
Confidence Interval for Population Mean
Excel Econometrics Tutorials
Multiple Regression Analysis
Estimation and InferenceTime Series Analysis
- Exponential Smoothing Forecasting
- Plotting Linear Trend and Forecasting
- Monthly Data De-Trending, Seasonal Index & Forecasting
- Linear, Exponential and Quadratic Trend
- Excel Tutorial for Normal Distributions
Data Analysis


