De-Broglie's Hypothesis | Chemistry Assignment Help
De-Broglie's Hypothesis
The French physicist Louis de Broglie made a bold assertion in 1923. Considering Einstein's relationship of wavelength lambda to momentum p, de Broglie proposed that this relationship would determine the wavelength of any matter, in the relationship:
lambda = h / p Where h is Planck's constant and p is momentum.
This wavelength is called the de Broglie wavelength.
According to de Broglie, an electron of mass ‘m’ moving with a velocity ‘v’ should be associated with a wave having wave length (lambda). This wave length and velocity are related by the following mathematical equation =>
…(1)
Where h is the Planck's constant and mv is the momentum of the moving particle. Equation is known as de Broglie relationship and can be written as 
or mv µ 
…(2)Equation (2) is another form of de Broglie relationship and this can be stated in words as “The momentum of a moving particle is inversely proportional to the wave-length of the waves associated with it.”
Proof of de Broglie Equation
Let us first consider the case of a photon. If we consider it to be a wave of frequency n, its energy is given byE = hn …(3)
If we now consider it as a particle of mass m, its energy is given by
E = mc2 …(4)
From equation (3) and (4), we get
hn = mc2 …(5)
As the photon travels in free space with velocity of light c, its momentum p is given by
P = mass ´ velocity = mc …(6)
On dividing equation (5) by (6), we get
or
[
c = vl = Frequency ´ wave length] or
…(7) de-Broglie assumed that the above relation holds good for material particles like electrons, and hence for electrons eq. (7) becomes as
…(8)Where m is the mass, v the velocity, l the wave length and p the momentum of an electron. Equation (8) is same as equation (1).
De-Broglie Relationship and Bohr's Theory
Application of the de-Broglie's relationship to a moving electron around a nucleus puts some restrictions on the size of orbits. It means that electron is not a mass particle moving in a circular path but is instead a standing wave train (non-energy, radiating motion) extending around the nucleus in the circular path as shown below: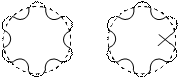
For the wave to remain continually in phase, the circumference of the orbit should be an integral multiple of wavelength l i.e.,
2pr = nl …(9)
Where r is the radius of the orbit and n is a whole number.
From equation (8), we get
l = h/mv …(10)
Substituting the value of l in equation (9), we get
or 
… (11) Which is the same as Bohr's second postulate. From equation (11) it follows that “Electron can move only in such orbits for which the angular momentum must be an integral multiple of h/2p. If the circumference is bigger or smaller than the value as given by equation (11), it means that the wave is not in the phase as shown in figure(2). Thus, de-Broglie relation provides a theoretical basis for the Bohr’s second postulate.
Our Customer Service Support Center
Assignmenthelp.net's Services – ready to help students around the clock (24/7 technical support) Live Supports by Phone, Chat or E-mail (support@assignmenthelp.net). The assignments, we provide is plagiarism free and offer free download facility of Chemistry/Physics tutorials as well. Expert online chemistry tutors at Assignmenthelp.net provide all sorts of help regarding your problems in chemistry(de-broglie's hypothesis, atomic structure) through e-mail and live chat.
To submit Chemistry Courses Click here
