Test Of Significance For Large Samples Assignment Help

In this section we will discuss the test of significance when samples are large. We have seen that for large values of n, the number of trials, almost all the distributions, eg., binomial, Poisson, Negative binomial, etc., are very closely approximated by normal distribution. Thus in this case we apply the normal test, which is based upon the following fundamental property of the normal probability curve.

If X ≈ n( μ, σ2), then z =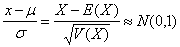

Thus from the normal probability tables, we have

P( -3 ≤ Z ≤ 3) = 0.9973 that is P(|Z|≤ 3 ) = 0.9973

1. è P(|Z|> 3 ) = 1- P( |Z| ≤ 3) = 0.0027

That is in all probability we should expect a standard normal variate to lie between ± 3.

---

Test Of Significance For Large Samples Assignment Help By Online Tutoring and Guided Sessions from AssignmentHelp.Net

---

Also from the normal probability tables, we get

P ( -1.96 ≤ Z ≤ 1.96 ) = 0.95 that is P(|Z| ≤ 1.96) = 0.95

1. è P(|Z| > 1.96 ) = 1 – 0.95 = 0.05
2. è P(|Z| ≤ 2.58 ) = 0.99
3. è P(|Z| > 2.58 ) = 0.01

Thus the significant values of Z at 5% and 1% level of significance for a two tailed test are 1.96 and 2.58 respectively.

Thus the steps to be used in the normal test are as follows:

1. (i) Compute the test statistic Z under H0.
2. (ii) If |Z| >3, H0 is always rejected.
3. (iii) If |Z| ≤3, we test its significance at certain level of significance, usually at 5% and sometimes at 1% level of significance. Thus, for a two tailed test if |Z| >1.96, H0 is rejected at 5% level of significance.

Similarly if |Z| > 2.58, H0 is contradicted at 1% level of significance and if |Z| ≤ 2.58, H0 may be accepted at 1% level of significance.

From the normal probability tables, we have:

P(Z >1.645) = 0.5 – P (0 ≤Z ≤1.645)

= 0.5 – 0.45

= 0.05

P(Z> 2.33) = 0.5 - P(0 ≤Z ≤2.33)

= 0.5 – 0.49

= 0.01

Hence for a single tail test we compare the computed value of |Z| with 1.645 and 2.33 and accept or reject H0 accordingly.

Email Based Homework Help in Test Of Significance For Large Samples

To submit Test Of Significance For Large Samples assignment click here.

Following are some of the topics in Sampling and Large Sample Tests in which we provide help: