Statistics Assignment Help With Critical Values Or Significant Values

10.7.2 Critical values or significant values:

The value of test statistic which separates the critical region and the acceptance region is called the critical value or significant value. It depends upon:

1. (i) The level of significance used, and
2. (ii) The alternative hypothesis, whether it is two tailed or single tailed.

As has been pointed out earlier, for large samples, the standardized variable corresponding to the statistic t viz. :

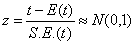------------------------(a)

Asymptotically as n à ∞. The value of Z given by (a) under the null hypothesis is known as test statistic. The critical value of the test statistics at level of significance α for a two- tailed test is given by Zα where Zα is determined by the equation

P(|Z|> Zα) = α ------------------(1)

That is Zα is the value so that the total area of the critical region on both tails is α. Since normal probability curve is a symmetrical curve, from (1), we get

P(Z > Zα) + P(Z < -Zα) = α

1. è P (Z > Zα) + P(Z >Zα) = α
2. è 2P (Z > Zα) = α
3. è P( Z > Zα) = α/2

That is the area of each tail is α/2. Thus Zα is the value such that area to the right of Zα is α/2 and to the left of - Zα is α/2.

In case of single tail alternative, the critical value Zα is determined so that total area to the right of it is α and for left tailed test the total area to the left of - Zα is α.

Thus the significant or critical value of Z for a single tailed test (left or right) at level of significance ‘α’ is same as the critical value of Z for a two tailed test at level of significance ‘2α’.

Email Based Homework Help in Critical Values Or Significant Values

To submit Critical Values Or Significant Values assignment click here.

Following are some of the topics in Sampling and Large Sample Tests in which we provide help: