Statistics Assignment Help With One Tailed And Two Tailed Tests

In any test, the critical region is represented by a portion of the area under the probability curve of the sampling distribution of the test statistic.

A test of any statistical hypothesis where the alternative hypothesis is one tailed is called a one tailed test. For example, a test for testing the mean of a population

H0: μ = μ0

Against the alternative hypothesis:

H1: μ > μ0 (right tailed) or H1: μ < μ0 (left tailed)

Is a single tailed test. In the right test (H1: μ > μ0), the critical region lies entirely in the right tail of the sampling distribution or 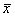, while for the left tail test (H1: μ < μ0), the critical region is entirely in the left tail or the distribution.

A test of statistical hypothesis where the alternative hypothesis is two tailed such as:

H0: μ = μ0, against the alternative hypothesis H1: μ ≠ μ0 is known as two tailed test and in such a case the critical region is given by the portion of the area lying in both the tails of the probability curve of the test statistic.

In a particular problem, whether one tailed or two tailed test is to be applied depends entirely on the nature of the alternative hypothesis. If the alternative hypothesis is two tailed we apply two tailed test and if alternative hypothesis is one tailed, we apply one tailed test.

Email Based Homework Help in One Tailed And Two Tailed Tests

To submit One Tailed And Two Tailed Tests assignment click here.

Following are some of the topics in Sampling and Large Sample Tests in which we provide help: