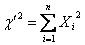Non Central Chi Square distribution Assignment Help

11.11 Non Central Chi Square distribution:

The chi-square distribution defined as the sum of the squares of independent standard normal variates is often referred to as the central chi-square distribution. The distribution of the sum of the squares of independent normal variates each having unit variance but with possibly non zero means is known as non-central chi-square distribution. Thus if Xi, (i=1,2,…,n)are independent N(μi, 1), random variables then

Has the non central chi-square distribution with n degrees of freedom. Intuitively, this distribution would seem to depend upon the n parameters μ1, μ2,…….., μn but it will be seen that it depends on these parameters only through the non-centrality parameter.

---

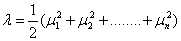
Non Central Chi Square distribution Assignment Help By Online Tutoring and Guided Sessions at AssignmentHelp.Net

---

And we write, .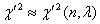

Email Based Homework Help in Non Central Chi Square distribution

To submit Non Central Chi Square distribution assignment Click here.

Following are some of the topics in Exact Sampling distributions in which we provide help: