Exact Sampling distributions Assignment Help
11.1 Chi-Square Variate:
The square of a standard normal variate is known as chi-square variate with 1 degree of freedom
Thus if X≈ N(μ, σ2), then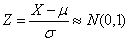 
And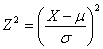 
is a chi-square variate with 1 degree of freedom.
In general, if Xi, (i = 1, 2, ……, n) are n independent normal variates with mean μi and variance σi2, (i = 1, 2, ……, n), then
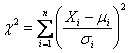is a chi-square variate with n degrees of freedom.
Exact Sampling distributions Assignment Help Through Online Tutoring and Guided Sessions from AssignmentHelp.Net
Email Based Homework Help in Exact Sampling distributions
To submit Exact Sampling distributions assignment click here.
Following are some of the topics in Exact Sampling distributions in which we provide help:
- Exact Sampling Distributions
- Derivation Of The Chi Square Distribution
- Moment Generating Function Of x2Distribution
- Cumulant Generating Function Of x2Distribution
- Limiting Form Of x2Distribution For Large Degrees Of Freedom
- Characteristic Function Of x2Distribution:
- Conditions For The Validity Of Chi Square Test
- Brandt And Snedecor Formula For 2Xk Contingency Table
