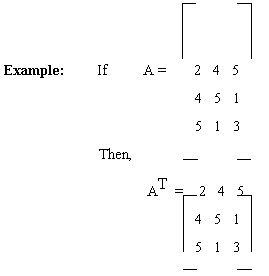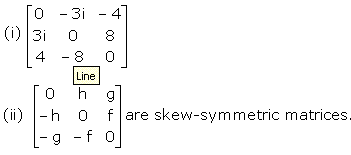Math Assignment Help With Symmetric And Skew-Symmetric Matrix

3.5 Symmetric and Skew-Symmetric matrix

3.5.1 Symmetric matrix: A square matrix A = [aij] is said to be symmetric if its (i, j)^th element is the same as its (j, i)^th element.

i.e. A = A^T

A = A^T

Therefore, A is symmetric matrix.

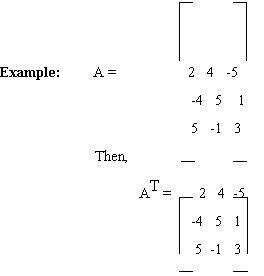
3.5.2 Skew symmetric matrix: A square matrix A = [aij] is said to be skew-symmetric if the (i, j)^th element of A is the negative of the (j, i)^th element of A

i.e. A ^T = -A

Therefore, A^T = -A

Properties of Symmetric and skew-symmetric matrix

1. i) A square matrix A is said to be skew-symmetric if A' = -A.
2. ii) The diagonal elements of a skew-symmetric matrix are all zero.

Examples:

iii) It may be checked that ½ (A +A^T) is symmetric and ½ (A - A^T) is skew-symmetric for every square matrix A. iv) A = (A +A^T)/2 + (A - A^T)/2

That is any square matrix can be expressed as the sum of a symmetric matrix and a skew-symmetric matrix.

v) A matrix which is both symmetric and skew symmetric is a zero matrix.

Email Based Homework Help in Symmetric And Skew-Symmetric Matrix

To submit Symmetric And Skew-Symmetric Matrix assignment click here.

Following are some of the topics in Matrices And Determinants in which we provide help: