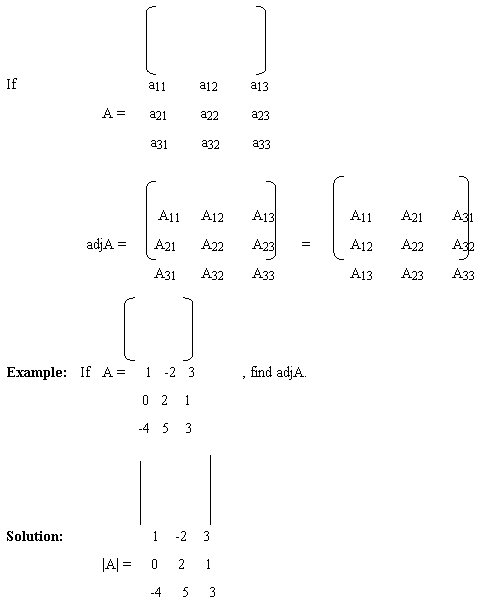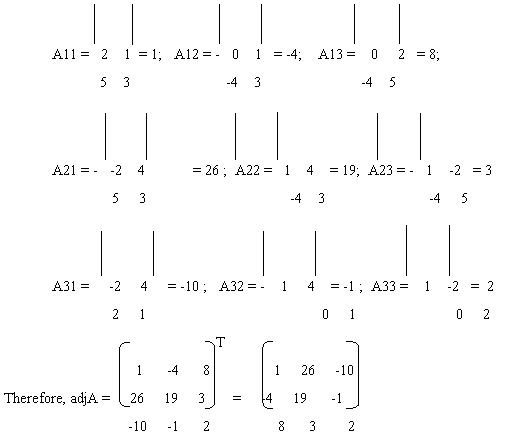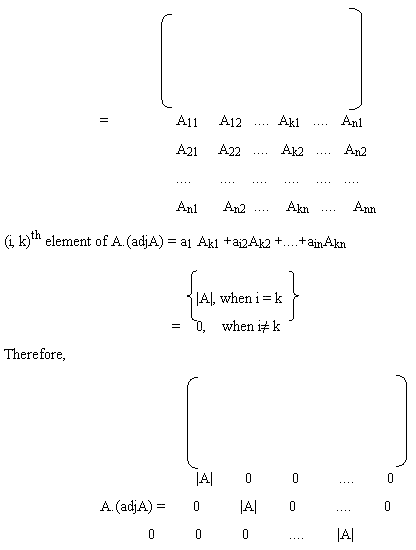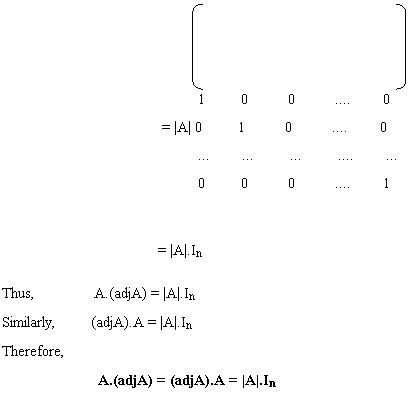Math Assignment Help With Adjoint And Inverse Of A Matrix

3.7 Adjoint and Inverse of a Matrix:

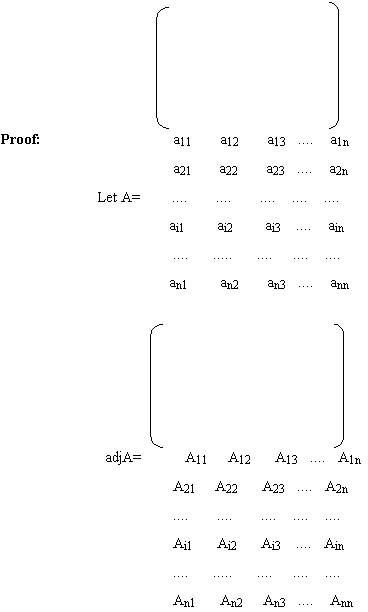
3.7.1 Adjoint of a matrix: Let a square matrix A = [aij] of order n and Aij denote the co-factor of aij in |A|, then the adjoint of is defined as:

adjA = [Aij] nxn

Hence, adjA is the transpose of the matrix of corresponding co-factors of elements of |A|.

Then the co-factors of elements of |A| are;

Theorem1: If a square matrix A is of order n, then prove that

A.(adjA) = (adjA).A = |A|.In

Email Based Homework Help in Adjoint And Inverse Of A Matrix

To submit Adjoint And Inverse Of A Matrix assignment click here.

Following are some of the topics in Matrices And Determinants in which we provide help: