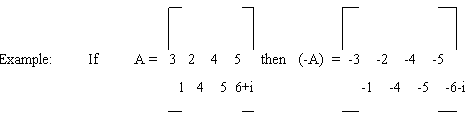Math Assignment Help With Addition Of Matrices

Some results of Addition of Matrices:

Theorem 1: Matrix addition is Commutative, i.e.

A+B = B+A for all comparable matrices A and B

Proof: Let A = [ aij]m x n B = [ bij]m x n

Then,

A+B = [ aij]m x n + [ bij]m x n

= [ aij + bij ]m x n (by definition of addition matrices)

= [ bij+aij ]mxn (since addition of numbers is commutative)

= [bij]mxn + [ aij]mxn = B+A

Hence,

A+B = B+A

Theorem 2: Matrix addition is associative. i.e

(A+B)+C = A+(B+C) for all comparable matrices A,B,C.

Proof: Let A = [ aij]m x n , B = [ bij]m x n C = [ cij]m x n

Then,

(A+B)+C = ([ aij]m x n + [ bij]m x n) + [ cij]m x n

= [ aij + bij ]m x n + [ cij]m x n

=[( aij + bij)+ cij]m x n

=[aij + (bij + cij)]m x n

=[ aij]m x n + [(bij + cij)]m x n

= A+(B+C)

Hence,

(A+B)+C= A+(B+C)

Theorem 3: If A is an mxn matrix and O is an mxn null matrix, then

A+O =O+A =A

Proof: Let A = [ aij]m x n O = [ bij]m x n’

Where, bij = 0

Then,

A+O = [ aij]m x n + [ bij]m x n’

= [ aij + bij ]m x n

= [ aij + 0 ]m x n

= [ aij]m x n

= A

Therefore,

A+O = A

Similarly,

O+A = A

Hence,

A+O=O+A=A

3.3.2 Negative of a matrix:

For a given matrix A, its negative is obtained by replacing each element with its corresponding additive inverse.

Email Based Homework Help in Addition Of Matrices

To submit Addition Of Matrices assignment click here.

Following are some of the topics in Matrices And Determinants in which we provide help: