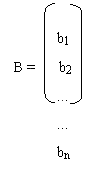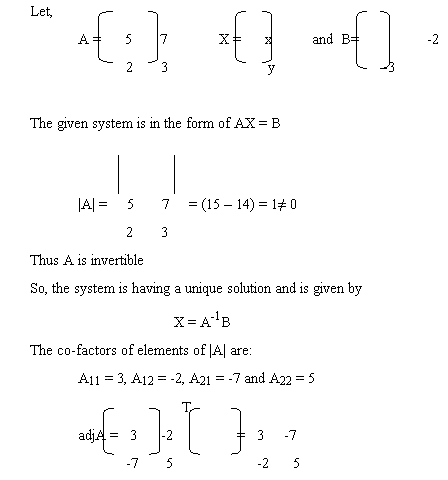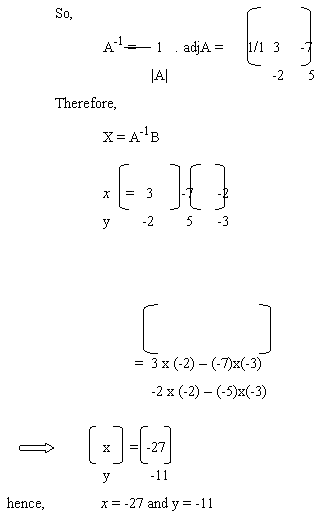Math Assignment Help With System Of Linear Equation

3.7.3 System of linear equation:

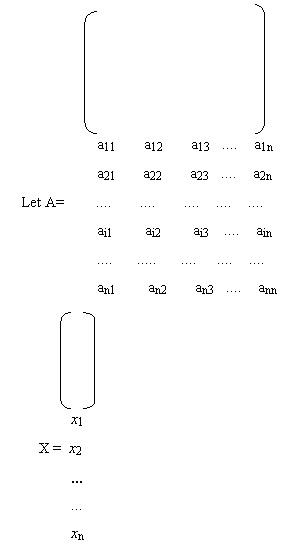
3.7.3.1 Linear equation in matrix notation: take the following system of linear equation;

a11x+a12x+....+a1_nxn

= b1

a21x+a22x+....+a2_nx_n = b2

........ .... .... ... ... ... ....

... ... ... ... .... .... .... ....

a_n1x+a_n2x+....+a_nnx_n = b_n

and,

The above system can also be written in the form;

AX = B

It can be rearranged as;

-1B

Let X = X1 and X = X2 be two solutions of AX = B

So,

AX1 = B and AX2 = B

Therefore,

AX1 = AX2

Since A being invertible, by cancellation law, we have;

X1 = X2

Hence the given system of equation has unique solution.

Criterion for a given system of equation to have unique solution:

i) If |A| ≠ 0, then the system is consistent and has a unique solution and is given by

X = A^-1B

ii) If |A| = 0 and (adjA) B ≠ 0, then the system is inconsistent.
iii) If |A| = 0 and (adjA) B = 0 then the system is consistent and has infinitely many solution.

Example: Using matrix method, solve the system of linear equation;

5x + 3y + 2 = 0

2x + 3y + 3= 0

Solution: the given set equations are

5x + 7y + 2 = 0

2x + 3y + 3= 0

To submit System Of Linear Equation assignment click here.