The Time Value of Money Assignment Help

1. Home
2. The Time Value of Money

By the concept of time value of money we mean that $1 received in the future is worth less than $1 today. The value today (in present) of a sum of money in future period is calculated using the present value analysis. The present value of an amount received in the future is equal to the sum of money an investor would have to invest today, at the prevailing interest rate, to end up with that amount in future.

The present value analysis is the reverse of future value analysis. Suppose an investor deposits $100 today in a bank account that pays 5 percent interest per year, at the end of the year the investor will have $105 in his bank account. Thus, $105 is the future value of $100 today. Alternately we can state that $100 is the present value of $105 received in the future, after one year.

The present value of a future sum of money depends on

• (1) The interest rate
• (2) The duration of time until the sum will be received in the future.
• (3) The size of the future amount.

For example, Consider an investor deposits $1,000 in the bank today and the bank agrees to pay her an interest rate of 8 percent per year. After one year, she will have (1+.08)×$1,000=$1,080

The $1000 is the principal sum that the investor gets back, and the .08*1000 is the interest payment on the principal sum. At the end of two years, she will have [(1+.08)×$1,000]×(1+.08) = (1+.08)² × $1,000 = $1,166.40

The component (1+.08) raised to the power of 2 shows that the original amount is invested for two years. The investor earns interest in the second year on the interest received in the first year.

Suppose a market rate of interest, i, is available to all borrowers and lenders. If the present amount to be invested at the interest rate is PV, the future value (FV) of the present amount in T years is FV = PV ×(1 + i)^T (8.1)

Solving the equation for PV in terms of FV, we get PV = FV/(1 + i)^T (8.2)

The present value (PV) of an amount (FV) received T years in the future when the interest rate is i percent per year. For example, if FV = $1,050, T = 1, and i = 5%, you will receive $1,050 one year in the future, and the prevailing interest rate is 5 percent. In this case, the present value of the future amount is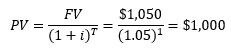

This means that if the interest rate is 5 percent the investor will need to invest $1000 today to receive $ 1,050 a year from now.

The present value equation depicts the time value of money.

The farther into the future a given dollar amount is to be received (the greater T is), the lower its present value. In other words, the present value of a future amount is inversely related to the time in which that amount is received.

The present value of an amount to be received at a given point in the future is inversely related to the interest rate. As the interest rate rises, the present value of a given future amount falls. Conversely, the lower the interest rate, the greater the present value.

Need help with time value of money calculations or bond price valuation assignments for finance homework? Get in touch with our finance homework help tutors.

Present Value Calculation for a series of Future Values

Suppose varying amounts are to be received over time; FV1 will be received at the end of the first year, FV2 at the end of the two years, and so on for T years. The present value of this stream of future payments is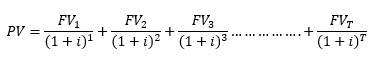

The first term on the right hand side of the equality is the present value of the first future payment. To this we add the present value of the payment received two years in the future, three years in the future, and so on. By adding together the present value of each future payment, we end up with the present value of the series of future payments.

Sample Example for Present Value Calculation

Suppose your Aunt wishes to purchase a $50,000 worth of Real-Estate after three years from now. If the interest rate is 5 percent, how much will she have to deposit in the bank today to be able to purchase the real-estate three years from now?

She must deposit the sum of money such that after three years its future value will be $50,000. Thus, she needs to deposit the present value of the $50,000 needed in three years. Given the 5 percent interest rate, this amount will be calculated as: PV = $50,000/(1.05)³ = $43,191.88

Read ahead to learn more about bond valuation and calculation of bond prices and bond yields based on the concept of time value of money.

The Time Value of Money Introduction

---

The Time Value of Money Assignment Help By Online Tutoring and Guided Sessions from AssignmentHelp.Net

---

To understand the concept let us straight away take an example.

Suppose we have $ 100 with us and we deposit it in a bank which pays 6% annual interest. Then after 1 year the amount in bank will be:

$ 100 + $ 100 * 6 % interest = 100+ 6 = $ 106

If we keep the amount in bank for 1 more year then the amount in bank will be:

$ 106 + $ 106 * 6% interest = 106 + 6.36 = $.112.36

If we look carefully, we will observe that in second year the interest amount has increased by $ 0.36, we call as interest on interest. That is interest on $ 6 @ 6% which gives us $. 0.36.

So we can safely say that for an investment horizon of t years, the original $ 100 investment will grow to $. 100 × (1.06)t. For an interest rate of r and a horizon of t years, the future value of our investment will be:

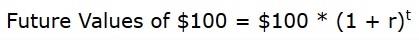
Earning interest on interest is called compounding or compound interest. In contrast, if the bank calculated the interest only onour original investment, we would be paid simple interest.

The following table will give us a more clear view of the interest on interest principle:

Year Balance at the Start Interest earned Balance at the end

1 $ 100.00 .06 × $ 100.00 = $ 6.00 $ 106.00

2 $ 106.00 .06 × $ 106.00 = $ 6.36 $ 112.36

3 $ 112.36 .06 × $ 112.36 = $ 6.74 $ 119.10

4 $ 119.10 .06 × $ 119.10 = $ 7.15 $ 126.25

5 $ 126.25 .06 × $ 126.25 = $ 7.57 $ 133.82

Here we can see that after 5 years the interest earned is $ 33.82. Had we not taken the concept of compound interest the interest earned for this period would have been only $ 30.

Following are some of the topics in The Time Value of Money in which we provide help: