Physics Assignment Help With Gravitational Field

6.2 Gravitational Field

It is the region around a mass upto which another mass can experience its influence.

Gravitational field is described by the two quantities as shown in diagram given below :

(a) Gravitational field intensity

(b)Gravitational potential



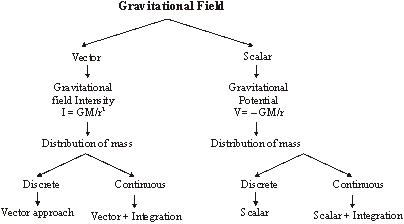
6.2.1 Gravitational Field Intensity

The intensity of gravitational field at a point is the force acting per unit mass of a test particle kept at that point i.e. . The direction of  is same as that of .

Since

\

i.e.

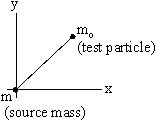
It is a unit vector whose direction is always towards the source mass.

6.2.2 Field Due to Uniform Thin Spherical Shell

Consider a thin spherical shell or radius R, mass M and of negligible thickness. Out of the spherical shell we consider a small ring of thickness Rdq. The shaded ring has mass dm=(M/2)sinq dq. The field at p due to this ring is

From DOAP

z2 = a2 + r2 – 2ar cosq

or 2zdz = 2ar sinq dq

or sinq dq = zdz / a.r

Also, from DOAP,

a2 = z2 + r2 – 2zr. cosa

Thus,

or

Case I (p is outside the shell, r > a)



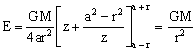
We see that the shell may be treated as a point particle of the same mass placed at its centre to calculate the gravitational field at an external point.

(inside the shell, r < a).



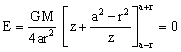
We see that field inside a uniform spherical shell is zero.

6.2.3 Relation between gravitational field and potential

Suppose the gravitation field at a point due to a given mass distributed is . By definition the force on a particle of mass m when it is at distance.



As the particle is displaced from the work done by the gravitational force on it is



The change in potential energy during this displacement is



The change in potential is, by equation

... (1)

If we work in Cartesian coordinates, we can write



and

So that

Equation (1) may be written as

dV = – ex dx – ey dy – Ez dz

If y and z remain constant, dy = dz = 0

Thus,

Similarly, and

The symbol means partial differentiation with respect to x treating y and z to be constants.

Gravitational Potential

It is defined as the work done in moving unit mass from infinity to that point against the field. If W work is done in moving a mass m then V = W/m.

Its units are Joule/kg. It is a scalar quantity. its proper sign is negative. In integral from gravitational potential is given by . The gravitational potential on the surface of a sphere of mass M & radius R is, V = – GM / R

Email Based Assignment Help in Gravitational Field

We are the leading online Assignment Help provider. Find answers to all of your doubts regarding the Gravitational Field. Assignmenthelp.net provide homework, Assignment Help to the school, college or university level students. Our expert online tutors are available to help you in Gravitational Field. Our service is focused on: time delivery, superior quality, creativity and originality.

To submit physics Gravitational Field assignment click here.

Following are some of the areas in physics Gravitational Field which we provide help: