Statistics Assignment Help With Curve Fitting By Orthogonal Polynomial

Suppose that the polynomial of pth degree of Y on X is

yx= a0+ a 1 x+ a 2 x2+……………..+ a p xp

the normal equations for determining the constants ai’s are obtained by the principle of least squares by minimizing the residual or error sum of squares

The use of equation is subject to one serious drawback. If we have a set of data and apart from inspection if there is no guide regarding the order of the polynomial to be fitted, the only way left to us is to try curves of order 1,2,3. until we reach the point where further terms do not improve the fit. Every time we add a new term, the aj,’s given by change and accordingly the determinantal arithmetic has to be done afresh. For example, if we want to fit a polynomial curve of third or higher degree to the same data then we cannot use the coefficients which we computed while fitting a second degree parabola. To overcome this drawback prof. R.A. Fisher suggested a method which involved the fitting of orthogonal polynomials by the principle of least squares, so that each term is independent of the other,. i.e. each of the coefficients in the polynomial is independent of the other so that each of them can be calculated independently. In this method, the coefficients computed earlier remain the same and we have to compute the coefficient only for the added term.

7.5.1 Orthogonal Polynomials:

Two polynomials P1 (x) and P2 (x) are said to be orthogonal to each other if

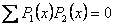
Where summation is taken over a specified set of values of x. if x were a continuous variable in the range from a to b, the condition for orthogonality give

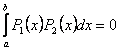
Email Based Homework Help in Curve Fitting By Orthogonal Polynomial

To submit Curve Fitting By Orthogonal Polynomial assignment click here.

Following are some of the topics in Curve Fitting in which we provide help: