7. Curve Fitting And Principle Of least Squares

7.1 Curve Fitting:

Let (xi,yi) ; I =1,2,3,……….n be a given set of n pairs of values, X being independent variable and Y the dependent variable, the general problem in curve fitting is to find, if possible, an analytic expression of the form y=f(x), for the functional relationship suggested by the given data.

Fitting of curves to a set of numerical data is of considerable importance theoretical as well as practical. Theoretically it is useful in the study of correlation and regression, e.g., lines of regression can be regarded as fitting of linear curves to the given bivariate distribution. In practical statistics it enables us to represent the relationship between two variables by simple algebraic expressions, e.g., polynomials, exponential or logarithmic functions. Moreover, it may be used to estimate the values of one variable which would correspond to the specified values of the other variable.

7.1.1 Fitting of a straight line:

Let us consider the fitting of a straight line

---

Curve Fitting Assignment Help Through Online Tutoring and Guided Sessions from AssignmentHelp.Net

---

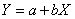
To a set of n points (xi,yi); i =1,2,3………,n. Equation represents a family of straight lines for different values of the arbitrary constants ‘a’ and ‘b’. The problem is to determine ‘a’ and ‘b’ so that the line is the line of “best fit”.

Email Based Homework Help in Curve Fitting

To submit Curve Fitting assignment click here.

Following are some of the topics in Curve Fitting in which we provide help: