Functions and Domain Assignment Help
Introduction to Function, Domain
Function: A function is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. An example is the function that relates each real number x to its square x2.
Notation:- A function f with domain X and codomain Y is commonly denoted by
Functions and Domain Assignment Help By Online Tutoring and Guide Sessions at AssignmentHelp.Net
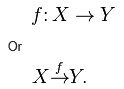
Basic properties:
- Image and pre image
- Injective and surjective functions
- Function composition
- Identity function
- Restrictions and extensions
- Inverse function
Types of functions
Real-valued functions
- An affine function f(x) = ax + b.
- Trigonometric function e.g., sin(x), cos(x)
- Continuous function
- A quadratic function f(x) = ax2 + bx + c
Further types of functions:
- differentiable, integrable
- polynomial, rational
- algebraic, transcendental
- odd or even
- convex, monotonic
- Holomorphic, meromorphic, entire
- vector-valued
- computable
Domain:
The domain of a function is the set of "input" or argument values for which the function is defined. The set of values the function takes is termed the image of the function, which is sometimes also referred to as the range of the function. The domain of cosine is the set of all real numbers, while the domain of the square root consists only of numbers greater than or equal to 0.
Definition of Domain:
f(x) = 1/x
has no value for f(0). Thus, the set of all real numbers, R, cannot be its domain. In cases like this, the function is either defined on R−{0} or the "gap is plugged" by explicitly defining f(0). If we extend the definition of f to
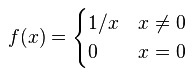
Then f is defined for all real numbers and its domain is R.
Example:
Function f : R -> R, f(x) = √x is defined for all x ≥ 0.
Math Function Types and Properties
