Math Function Types and Properties
Definition of a Function
Let D and C be two non-empty sets. A function f from set D to set C is a rule which associates to each element x∈D a unique element y∈C
The element y, written as y=f(x) is called image of x and x is called preimage of y .the set D is called the domain and C the co-domain of function f which is denoted by f:D→ C.
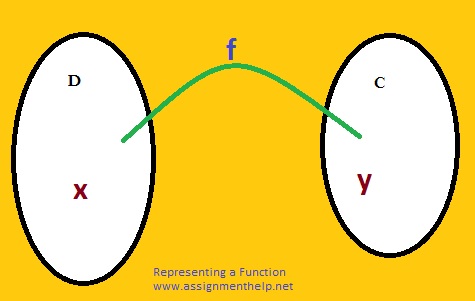
The set f(D)={f(x):x∈D}is called the range of the function f:D→ C.
Image of an element is unique in the sense that no element of D can have more than one image. However preimage may not be unique i.e., an element of C can have more than one preimage.
Every element in D has as image in C but every element in C may not have preimage in D. i.e., usually f(D) is proper subset of C.
What is a Real Function?
A function which has either R or one of its subsets as its range is called a real values function. Further ,if its domain is also either R or a subset of R ,It is called a real function.
What is one-to-one function?
A function f: D-> C is called one-to-one if distinct elements of D have distinct images in C, i.e.
x≠y => f(x)≠f(y) ∀ x,y∈D.
Or f(x)=f(y)=>x=y ∀ x,y∈D.
What is one-to-one onto function ?
A function f:D→C is said to be one-one and onto if f is both one-one and onto
What is an Identity Function ?
Identify Function: Let R be the set of real numbers. Define the real Function
f:R→R
Such that y = f(x) = x ∀ x∈R
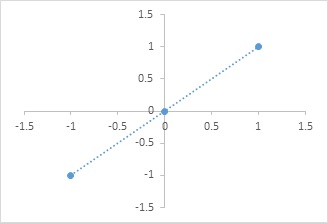
Domain of f = R
Codomain of f = R
Range of f = r
Also x ≠ y
=>f(x) ≠f(y) ∀ x∈
f is called identify function.
F is both one-one and onto.
What is a Constant Function Let R be the set of real numbers and c∈R be a fixed real number.
Define f:R→R
Such that y=f(x)=c ∀ x∈
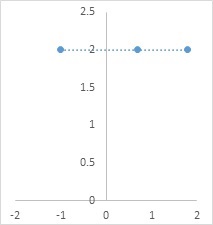
Domain of f = R
CoDomain of f = R
Range of f={c}
Also we have x≠y still f(x) f(y)
F is called the constant function
F is neither one-one nor onto
What is a Polynomial Function
A function f: R →R is sad to be polynomial function if for each x∈R we have
y=f(x) = a0 + a1 x + a2 x2 + ⋯ + an xn
Where n is non-negative integer and a0,a1,……..,an ∈R.
If a0 = a2 = a3 = ⋯= an = 0 and a1 = 1 the polynomial function become identity function.
If a1 = a2 =a3 = ⋯= an = 0 the polynomial function become constant function.
f(x) = x2 + 2x = 1 is a polynomial function.
f(x) = x3/2 + 4x is not a polynomial function.
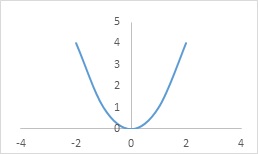
Consider the function
f: R →R.
Such that y = f(x) = x2 ∀ x ∈ R
Domain of f = R.
Range of f = {x ∈ R ∶ x ≥ 0}
f(-1) = (-1)2
= 1 = 12 = f(1)
f is neither one-one nor onto.
What are Rational Functions?
Define f: R →R.
Such that f(x)=p(x)/q(x) ,q(x) ≠ 0,x ∈ R
Where p(x) and q(x) are polynomials in x.
f(x) is called a rational function.
Consider f(x) = 1/x, x ≠ 0, x ∈ R
Domain of f = R - {0}
Range of f = R - {0}
f:R - {0} → R - {0} is both one-one and onto.
What is a Modulus Function ?
Modulus function
Define f: R →R.
Such that 
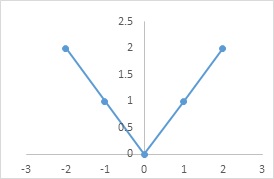
f is known as modulus function
f(-1)=|-1|=1=|1|=f(1)
Domain of f = R
Range of f={x ∈R∶x≥0}
f is neither one-one nor onto.
The following properties of modulus function cab be easily verified:
- (i) |xy|=|x||y| ∀ x,y ∈R
- (ii) |x|2 = x2 ∀ x ∈ R
- (iii) |x| ≤c if and only if-c≤x≤c
- (iv) -|x| ≤x ≤|x| ∀ x∈ R
- (v) |x+y| ≤|x|+|y| ∀ x ∈ R
- (vi) |(|x|-|y|)| ≤|x-y| ∀ x, y ∈ R
- (vii) |x-y| ≤|x|+|y| ∀ x,y∈ R
The interval (a+ϵ , a-ϵ) is nothing but ={x ∈R∶|x-a| < ε}
What is a Signum Function
f: R → R.
Such that 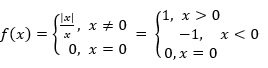
f is called signum function.
Domain of f = R.
Range of f={ -1,1,0}
F is neither one-one nor onto.

Define greatest integer Function
f: R →R.
Such that f(x) = [x] ∀ x ∈ R
=Greatest integer not greater than x
([1.1]=1&[0.9]=0&[1]=1
[-1.1]=-2&[-0.9]=-1&[-1]=-1)
Domain of f = R
Range of f = Z
f is neither one-one nor onto.