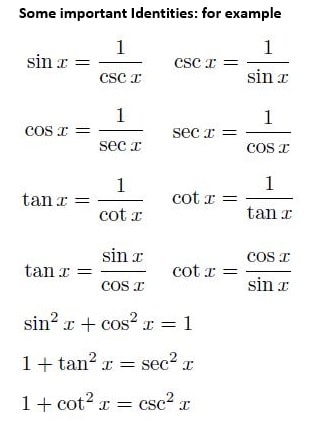Trigonometric Identities Assignment Help
Trigonometric Identities
The primary trigonometric identities which is given below
sine, = sin
cosine, = cos
tangent, = tan
cotangent, = cot
secant = sec
cosecant. = cosec
They represent the relationship created from a right triangle.
Imagine if a triangle has
a 90-degree angle, a 30-degree angle and a 60-degree angle.
Regardless of the size of the triangle, the relationship of the sides will be in proportion to each other.
(As the triangle gets bigger, the sides get bigger proportionately).
The trigonometric properties represent how sides are related to each other. Looking at the 30-degree angle, the opposite side will always be half as long as the hypotenuse (side opposite the right angle). The relationship of opposite to hypotenuse is represented with the sine function. The expression "the sine of 30 degrees is 1/2" is saying that the side opposite the 30-degree angle is half as long as the side opposite the right angle. If one of the sides is known, the other can be calculated. Likewise, if both side lengths are known, and the opposite / hypotenuse relationship is .5, it can be determined that the angle is 30 degrees.
Sine opposite with: hypotenuse = (opposite / hypotenuse)
Cosine adjacent with: hypotenuse = (adjacent / hypotenuse)
Tangent opposite with: adjacent = (opposite / adjacent)
Their opposite functions are
Cotangent,
Cosecant
and
Secant.
They have reserved relationships .
Cotangent =1 / Tangent,
Scant =1 / Cosine,
Cosecant = 1 / Sine,