Rhombic Icosahedron
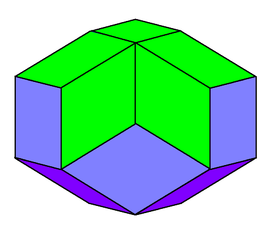
Rhombicicosahedron was discovered by Fedorov in 1885.
It belongs to a family of isohedral rhombic polyhedra that consists of prolate and obtuse rhombohedron. It is a convex polyhedra.
The faces of a rhombicicosahedron is made up of solids congruent rhombs whose diagonals are in golden ratio (also called as Golden Rhombi). A rhombicicosahedron can be constructed by gluing 5 rhombohedra of each kind.
A Rhombicicosahedron with edge length ‘a’ has Surface area and Volume as :
S = 8√5 a2
V = 2√(5+2√5) a3