Statistics Hypothesis Testing Assignment Help
Sample: Hypothesis Testing Paper
One and Two (or more) Sample Hypothesis Testing Paper. Using data from one of the data sets available through the “Data Sets” link on your page, develop one business research question from which you will formulate a research hypothesis to test one population parameter and another to test two (or more) population parameters. Formulate both a numerical and verbal hypothesis statement regarding each of your research issue.
Perform Hypotheses Tests using the five step model. Describe and interpret the results of the test, both in statistical terms and in conversational English. Include appropriate descriptive statistics.
Solution:
Research question: To find whether there is a significant difference between wins and salary of the baseball players.
There are two leagues denoted as
1 if American League and
0 if National League
We have separated the data set as
Data set
American League:
| Salary | alary -mil | Wins |
| 123505125.0 | 123.5 | 95.0 |
| 208306817.0 | 208.3 | 95.0 |
| 55425762.0 | 55.4 | 88.0 |
| 73914333.0 | 73.9 | 74.0 |
| 97725322.0 | 97.7 | 95.0 |
| 41502500.0 | 41.5 | 93.0 |
| 75178000.0 | 75.2 |
99.0 |
| 45.7 | 80.0 | |
| 56186000.0 | 56.2 | 83.0 |
| 29679067.0 | 29.7 | 67.0 |
| 55849000.0 | 55.8 | 79.0 |
| 69092000.0 | 69.1 | 71.0 |
| 87754334.0 | 87.8 | 69.0 |
| 36881000.0 | 36.9 | 56.0 |
Statistics Hypothesis Testing Assignment Help Through Online Tutoring and Guided Sessions from AssignmentHelp.Net
Claim: There is a significant difference between wins and salary- mil of the baseball players in American League.
Hypotheses:
Null Hypothesis:
Numerical Null Hypothesis:![]()
Verbal Null Hypothesis:![]() There is no significant difference between wins and salary- mil of the baseball players in American League.
There is no significant difference between wins and salary- mil of the baseball players in American League.
Alternative Hypothesis:
Numerical Alternative Hypothesis:![]()
Verbal Alternative Hypothesis:![]() There is a significant difference between wins and salary- mil of the baseball players in American League.
There is a significant difference between wins and salary- mil of the baseball players in American League.
Level of Significance:
α = 0.05
Decision rule:
If the p value is greater than the given level of significance we may accept the null hypothesis. Otherwise reject the null hypothesis.
Test Statistic: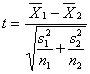
Using Megastat in Microsoft Excel Add- Ins:
Add- Ins à MegastatàHypothesis tests à Compare two independent groups
| Hypothesis Test: Independent Groups (t-test, pooled variance) | |||||
| Salary -mil | Wins | ||||
| 75.479 | 81.71 | mean | |||
| 45.930 | 13.07 | std. dev. | |||
| 14 | 14 | n | |||
| 26 | df | ||||
| -6.2357 |
difference (Salary -mil - Wins) | ||||
| 1,140.1793 |
pooled variance | ||||
| 33.7665 | pooled std. dev. | ||||
| 12.7626 | standard error of difference | ||||
| 0 | hypothesized difference | ||||
| -0.49 | t | ||||
| .6292 | p-value (two-tailed) | ||||
The test statistic value is -0.49.
The p value for the test statistic is 0.6292.
Conclusion:Since the p value of test statistic is greater than 0.05 level of significance we may accept the null hypothesis H0 at 5% level of significance. Hence, we conclude that there is no significant difference between wins and salary- mil of the baseball players in American League.
Research question: To find whether there is a significant difference between wins and salary of the baseball players.
Data set
National League:
| Salary | Salary -mil | Wins |
| 86457302.0 | 86.5 | 90.0 |
| 62329166.0 | 62.3 | 77.0 |
| 76799000.0 | 76.8 | 89.0 |
| 61892583.0 | 61.9 | 73.0 |
| 101305821.0 | 101.3 | 83.0 |
| 38133000.0 | 38.1 | 67.0 |
| 83039000.0 | 83.0 | 71.0 |
| 63290833.0 | 63.3 | 82.0 |
| 48581500.0 | 48.6 | 81.0 |
| 90199500.0 | 90.2 | 75.0 |
| 92106833.0 | 92.1 | 100.0 |
| 60408834.0 | 60.4 | 83.0 |
| 95522000.0 | 95.5 | 88.0 |
| 39934833.0 | 39.9 | 81.0 |
| 87032933.0 | 87.0 | 79.0 |
| 48155000.0 | 48.2 | 67.0 |
Claim: There is a significant difference between wins and salary- mil of the baseball players in National League.
Hypotheses:
Null Hypothesis:
Numerical Null Hypothesis:![]()
Verbal Null Hypothesis:
![]() There is no significant difference between wins and salary- mil of the baseball players in National League.
There is no significant difference between wins and salary- mil of the baseball players in National League.
Alternative Hypothesis:
Numerical Alternative Hypothesis:![]()
Verbal Alternative Hypothesis:![]() There is a significant difference between wins and salary- mil of the baseball players in National League.
There is a significant difference between wins and salary- mil of the baseball players in National League.
Level of Significance:
α = 0.05
Decision rule:
If the p value is greater than the given level of significance we may accept the null hypothesis. Otherwise reject the null hypothesis.
Test Statistic: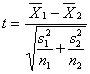
Using Megastat in Microsoft Excel Add- Ins:
Add- Ins à MegastatàHypothesis tests à Compare two independent groups
|
Hypothesis Test: Independent Groups (t-test, pooled variance) | |||
| Salary -mil | Wins | ||
| 70.949 | 80.375 | mean | |
| 20.669 | 8.831 | std. dev. | |
| 16 | 16 | n | |
| df | |||
| -9.4257 | difference (Salary -mil - Wins) | ||
| 252.5883 | pooled variance | ||
| 15.8930 | pooled std. dev. | ||
| 5.6190 | standard error of difference> | ||
| 0 | hypothesized difference | ||
| -1.68 | t | ||
| .1038 | p-value (two-tailed) | ||
The test statistic value is -1.68.
The p value for the test statistic is 0.1038.
Conclusion:
Since the p value of test statistic is greater than 0.05 level of significance we may accept the null hypothesis H0 at 5% level of significance. Hence, we conclude that there is no significant difference between wins and salary- mil of the baseball players in National League.
Regression analysis:
The general multiple regression is given by ![]()
where, y is the dependent variable,![]() ’s are independent variable,
’s are independent variable,![]() is the actual constant,
is the actual constant,![]() is the actual coefficient associated with ith independent variable,
is the actual coefficient associated with ith independent variable,![]() is the error term which models the unsystematic error of the y
is the error term which models the unsystematic error of the y
The above model can be written in matrix form as![]()
The General Goal of multiple regression is to determine which independent (explanatory) variables should be included in the model.
We want to first test each coefficient, ![]() where i=1,2,...,k, within the model, in order to determine if that individual parameter should be dropped from the model.
where i=1,2,...,k, within the model, in order to determine if that individual parameter should be dropped from the model.
Next we test the goodness of fit of the model.
Hypothesis Tests:![]()
![]()
Procedure:
First we estimate the model as![]()
where, ![]() is the estimated value of
is the estimated value of ![]() and
and ![]() .
.
For Testing Each ![]() :
:
The test statistic is given by![]()
where, ![]() is the standard error of the estimated coefficient
is the standard error of the estimated coefficient ![]() .
.
Goodness of fit test:
In order to test the goodness of fit test we generally compute R2, which lies between 0 and 1. As R2 tends to 1, we can say that the model is suitable for the data i.e. the model can explain the data very well.
Dependent variable:
X7- Wins
Independent variables:
X2- League
X3- Built
X4- Size
X5- Surface
X6- Salary- mil
X8- Attendance
X9- Batting
X10- ERA
X11- HR
X12- Error
X13- SB
Using Megastat in Microsoft Excel Add- Ins:
Add- Ins à MegastatàCorrelation/ Regression à Regression analysis
| Regression Analysis | ||||||
| R² |
0.857 | |||||
| Adjusted R² | 0.770 | n |
30 | |||
| R | 0.926 | k | 11 | |||
| Std. Error | 5.200 | Dep. Var. | Wins | |||
|
ANOVA table | ||||||
| Source | SS | df | MS | F | p-value | |
| Regression | 2,917.2794 | 11 | 265.2072 | 9.81 | 1.64E-05 | |
| Residual | 486.7206 | 18 | 27.0400 | |||
| Total | 3,404.0000 | 29 | ||||
| Regression output | confidence interval | |||||
| variables | coefficients | std. error | t (df=18) | p-value | 95% lower | 95% upper |
| Intercept | 74.6634 | 133.9145 | 0.558 | .5840 | -206.6805 | 356.0073 |
| League | -1.2494 | 2.3275 | -0.537 | .5980 | -6.1392 | 3.6404 |
| Built | -0.0274 | 0.0558 | -0.491 | .6291 | -0.1447 | 0.0899 |
| Size | -0.00000401 | 0.00020556 | -0.019 | .9847 | -0.00043588 | 0.00042787 |
| Surface | 0.5761 | 4.3135 | 0.134 | .8952 | -8.4863 | 9.6384 |
| Salary -mil | 0.0411 | 0.0667 | 0.615 | .5462 | -0.0992 | 0.1813 |
| Attendance | -0.00000085 | 0.00000317 | -0.267 | .7923 | -0.00000750 | 0.00000581 |
| Batting | 447.7443 | 200.5131 | 2.233 | .0385 | 26.4819 | 869.0067 |
| ERA | -13.6362 | 2.4171 | -5.642 | 2.37E-05 | -18.7143 | -8.5581 |
| HR | 0.0930 | 0.0338 | 2.755 | .0130 | 0.0221 | 0.1639 |
| Error | -0.1601 | 0.1246 | -1.285 | .2151 | -0.4218 | 0.1017 |
| SB | 0.0152 | 0.0361 | 0.422 | .6777 | -0.0605 | 0.0910 |
The regression equation is
Wins = 74.6634 - 1.2494 League - 0.0274 Built - 0.00000401 Size + 0.5761 Surface + 0.0411 Salary -mil - 0.00000085 Attendance + 447.7443 Batting -13.6362 ERA + 0.0930 HR -0.1601 Error + 0.0152 SB
The R-Sq(adj.) value is high. So the model has good fit. But the p-values for x2, x3, x4, x5, x6, x12 and x13 are greater than 0.05. So these coefficients are insignificant. There is thus a multicollinearity problem. So we drop these variables and regress x7 on x9, x10 and x11.
Regression Analysis: x7 versus x9, x10, x11
Dependent variable:
X7- Wins
Independent variables:
X9- Batting
X10- ERA
X11- HR
Using Megastat in Microsoft Excel Add- Ins:
Add- Ins à MegastatàCorrelation/ Regression à Regression analysis
| Regression Analysis | ||||||
| R² | 0.810 | |||||
| Adjusted R² | 0.788 | n | 30 | |||
| R | 0.900 | k | 3 | |||
| Std. Error | 4.988 | Dep. Var. | Wins | |||
|
ANOVA table | ||||||
| Source | SS | df | MS | F | p-value | |
| Regression | 2,757.1594 | 3 | 919.0531 | 36.94 | 1.60E-09 | |
| Residual | 646.8406 | 26 | 24.8785 | |||
| Total | 3,404.0000 | 29 | ||||
| Regression output | confidence interval | |||||
| variables | coefficients | std. error | t (df=26) | p-value | 95% lower | 95% upper |
| Intercept | 1.8499 | 35.0214 | 0.053 | .9583 | -70.1376 | 73.8374 |
| Batting | 492.4490 | 140.3025 | 3.510 | .0017 | 204.0532 | 780.8449 |
| ERA | -15.9575 | 1.6753 | -9.525 | 5.78E-10 | -19.4011 | -12.5139 |
| HR | 0.1035 | 0.0289 | 3.582 | .0014 | 0.0441 | 0.1628 |
The regression equation is
Wins = 1.8499 + 492.4490 Batting -15.9575 ERA + 0.1035 HR
Here all the p values of the coefficients are less than 0.05 i.e. ![]() are significant at 5 % level of significance. The R2 value is slightly reduced after dropping the variables and it is of not that much effect and hence the model is good.
are significant at 5 % level of significance. The R2 value is slightly reduced after dropping the variables and it is of not that much effect and hence the model is good.
Correlation:
Research question: To find whether salary have relationship with Attendance of the baseball players.
There are two leagues denoted as
1 if American League and
0 if National League
We have separated the data set as
Data set
American League:
| Salary -mil | Attendance |
| 123.5 | 2,847,798 |
| 208.3 | 4,090,440 |
| 55.4 | 2,108,818 |
| 73.9 | 2,623,904 |
| 97.7 | 3,404,636 |
| 41.5 | 2,014,220 |
| 75.2 | 2,342,804 |
| 45.7 | 2,014,995 |
| 56.2 | 2,034,243 |
| 29.7 | 1,141,915 |
| 55.8 | 2,525,259 |
| 69.1 | 2,024,505 |
| 87.8 | 2,724,859 |
| 36.9 | 1,371,181 |
Using Megastat in Microsoft Excel Add- Ins:
Add- Ins à MegastatàCorrelation/ Regression à Correlation Matrix
| Correlation Matrix | ||
| Salary -mil | Attendance | |
| Salary -mil | 1.000 | |
| Attendance | .895 | 1.000 |
| 14 | sample size | |
The correlation coefficient between salary- mil and attendance is 0.895. there is a strong positive correlation exist between the variables.
Null Hypothesis:
H0: ρ=0
H0: “no linear relationship” between the variables.
Alternative Hypothesis:
H1: ρ≠0
H1:“ linear relationship” between the variables.
Level of significance:
α = 0.05
Critical value:
At 5% level of significance t distribution with v = 14 - 2 degrees of freedom is 2.178813
Test statistic:
Under ![]()
![]() has a t distribution with v = n-2 degrees of freedom.
has a t distribution with v = n-2 degrees of freedom.
r= 0.895 and n = 14![]()
![]()
![]()
![]()
![]()
Conclusion:
Since the test statistic value is greater than the critical value there is no evidence to accept the null hypothesis at 5% level of significance. Hence we conclude that there is a relationship exist between the variables salary- mil and attendance.
Data set
National League:
| Salary -mil | Attendance |
| 86.5 | 2,520,904 |
| 62.3 | 2,059,327 |
| 76.8 | 2,805,060 |
| 61.9 | 1,923,254 |
| 101.3 | 2,827,549 |
| 38.1 | 1,817,245 |
| 83 | 3,603,680 |
| 63.3 | 2,869,787 |
| 48.6 | 2,730,352 |
| 90.2 | 3,181,020 |
| 92.1 | 3,542,271 |
| 60.4 | 1,852,608 |
| 95.5 | 2,665,304 |
| 39.9 | 2,211,323 |
| 87 | 3,100,092> |
| 48.2 | 1,914,385 |
Using Megastat in Microsoft Excel Add- Ins:
Add- Ins à MegastatàCorrelation/ Regression à Correlation Matrix
| Correlation Matrix | ||
| Salary -mil | Attendance | |
| Salary -mil | 1.000 | |
| Attendance | .693 | 1.000 |
| 16 | sample size | |
The correlation coefficient between salary- mil and attendance is 0.693. There is a strong positive correlation exist between the variables.
Null Hypothesis:
H0: ρ=0
H0: “no linear relationship” between the variables.
Alternative Hypothesis:
H1: ρ≠0
H1:“ linear relationship” between the variables.
Level of significance:
α = 0.05
Critical value:
At 5% level of significance t distribution with v = 16 - 2 degrees of freedom is 2.144787
Test statistic:
Under ![]()
![]() has a t distribution with v = n-2 degrees of freedom.
has a t distribution with v = n-2 degrees of freedom.
r= 0.693 and n = 16![]()
![]()
![]()
![]()
![]()
Conclusion:
Since the test statistic value is greater than the critical value there is no evidence to accept the null hypothesis at 5% level of significance. Hence we conclude that there is a relationship exist between the variables salary- mil and attendance.
Descriptive Statistics:
Using Megastat in Microsoft Excel Add- Ins:
Add- Ins à MegastatàDescriptive Statistics
| Salary -mil | Wins | Attendance | Batting | ERA | HR | Error | SB > | |
| count | 30 | 30 | 30 | 30 | 30> | 30 | 30 | 30 |
| mean | 73.064 | 81.000 | 2,496,457.93 | 0.26443 | 4.2847 | 167.23 | 102.00 | 85.50 |
| sample variance | 1,171.965 | 117.379 | 452,766,738,769.44 | 0.00005 | 0.3206 | 1,225.29 | 130.34 | 1,075.43 |
| sample standard deviation | 34.234 | 10.834 | 672,879.44 | 0.00728 | 0.5662 | 35.00 | 11.42 | 32.79 |
| minimum | 29.679067 | 56 | 1141915 | 0.252 | 3.49 | 117 | 86 | 31 |
| maximum | 208.30682 | 100 | 4090440 | 0.281 | 5.49 | 260 | 125 | 161 |
| range | 178.62775 | 44 | 2948525 | 0.029 | 2 | 143 | 39 | 130 |
| 1st quartile | 50.293 | 73.250 | 2,017,372.50 | 0.25900 | 3.7875 | 136.75 | 92.50 | 65.25 |
| median | 66.191 | 81.000 | 2,523,081.50 | 0.26400 | 4.2000 | 164.00 | 102.50 | 76.00 |
| 3rd quartile | 87.574 | 88.750 | 2,842,735.75 | 0.27000 | 4.5500 | 190.50 | 108.75 | 101.25 |
| interquartile range | 37.281 | 15.500 | 825,363.25 | 0.01100 | 0.7625 | 53.75 | 16.25 | 36.00 |
| mode | #N/A | 95.000 | #N/A | 0.27000 | 3.6100 | 130.00 | 106.00 | 45.00 |
The descriptive statistics for the whole team is given in the above table.
Inference for our research:
- From the analysis of comparing two independent groups we obtain the result as there is no significant difference between wins and salary- mil of the baseball players in American League.
- From the regression analysis we obtained the regression equation predicting the wins is
- From the correlation analysis we obtained the result as there is a relationship exists between the variables salary- mil and attendance of baseball players in American League.
- From the correlation analysis we obtained the result as there is a relationship exists between the variables salary- mil and attendance of the baseball players in National League.



