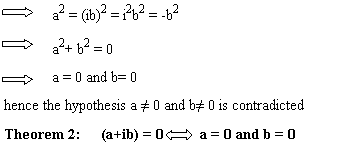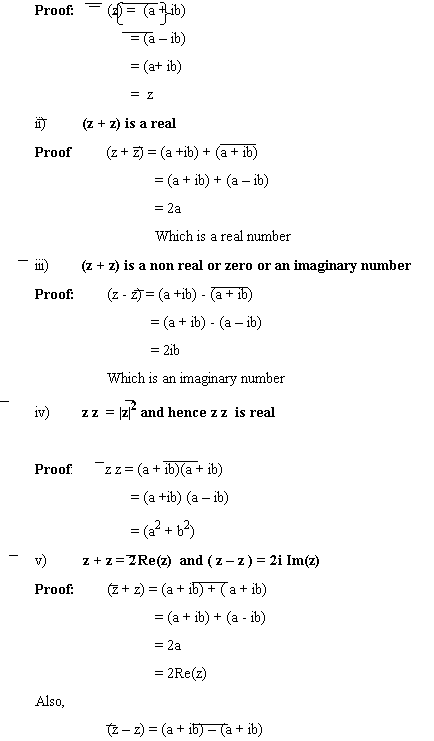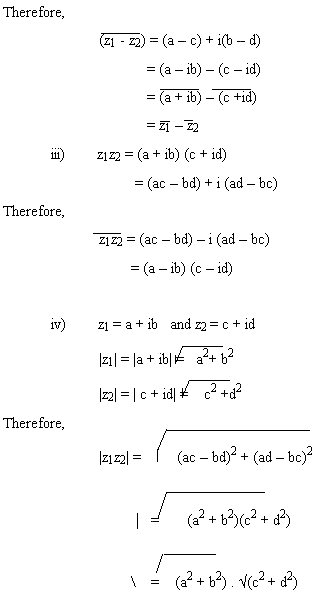Math Assignment Help With Properties Of Complex Number

1.5 Properties of Complex number:

Theorem 1. A real number can never be equal to imaginary number.

Proof: Let a≠ 0 and b≠ o are real numbers such that

Proof: (a + ib) = 0

a2 = (-ib)2 = i2b2 = -b2

a2 + b2 = 0

a = 0 and b = 0

Theorem 3: Two complex numbers are equal only when their real and imaginary parts are separately equal.

Proof: (a +ib) = (c + id)

(a + ib) – (c+id) = 0

(a – c) + i (b – d) = 0

(a – c) = 0 & (b – d) = 0

a = c & b = d

Theorem 4: If z є C, then;

i) Line(z) = z

Email Based Homework Help in Properties Of Complex Number

To submit Properties Of Complex Number assignment click here.

Following are some of the topics in Complex Number in which we provide help: