Statistics Assignment Help With Poisson Distribution

5.3 Poisson Distribution:

Poisson distribution was discovered by the French mathematician and physicist Simeon Denis Poisson who published it in 1837. Poisson distribution is a limiting case of the binomial distribution under the following conditions.

(i) n, the number of trials is indefinitely large, i.e., nà ∞.

(ii) p, the constant probability of success for each trial is indefinitely small, i.e., pà 0.

(iii) np = λ, is finite. Thus p = λ/n, q = 1-λ/n, where λ is a positive real number.

A random variable X is said to follow a Poisson distribution if it assumes only non-negative values and its probability mass function is given by

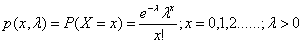
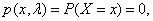otherwise

Here λ is known as the parameter of the distribution.

We shall use the notation X~ P(λ) to denote that X is a Poisson variate with parameter λ.

Email Based Homework Help in Poisson Distribution

To submit Poisson Distribution assignment Click here.

Following are some of the topics in Theoretical Discrete Distributions in which we provide help: