Statistics Assignment Help

1.2 Measures Of Measures Of Dispersion, Skwness And Kurtosis

The measures of dispersion is the defined as the how the set of observations dispersed or scattered. The measures of dispersion are:

• Range
• Quartile deviation or semi – interquartile range
• Mean deviation
• Standard deviation

1.2.1 Range:

The range is the difference between the largest observation and smallest observation.

Range = X Maximum – X Minimum

1.2.2 Quartile deviation or semi – interquartile range:

The quartile deviation is a measure describes about the 50 % of the data. The quartile deviation is denoted as Q.



Where Q3is the third quartile and Q1is the first quartile

1.2.3 Mean deviation:

Mean deviation explains about the deviation of the whole observation and it is a better measure than range and quartile deviation.

Mean deviation from the average is given as

Mean deviation =

Where fi is the frequency for the observation, Xi is the variables and N is the number of observations.

1.2.4 Standard deviation:

The standard deviation is the positive square root of the arithmetic mean of the squares of the deviations of the given values from their arithmetic mean. The population standard deviation is denoted as σ and the root mean square deviation as s.



Where (X bar) is the arithmetic mean, fi is the frequency for the observation, Xi is the variables and N is the number of observations.

The square of the standard deviation is called the variance

The root mean square deviation is

Where A is any arbitrary number, fi is the frequency for the observation, Xi is the variables and N is the number of observations.

The mean square deviation is

The standard deviation for the grouped or continuous frequency distribution is

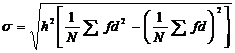
Where f is the frequency for the observation, Xi is the variables, N is the number of observations, A is an arbitrary point and h is the common magnitude.

Email Based Homework Help in Measures Of Measures Of Dispersion

To submit Measures Of Measures Of Dispersion assignment click here.

Following are some of the topics in Descriptive Statistics in which we provide help: