Statistics Assignment Help With Fishers Z Transformation

To test the significance of an observed sample correlation coefficient from an uncorrelated bivariate normal population, t – test is used. But in random sample of size ni, from a bivariate normal population in which ρ ≠ 0, Prof. R.A. Fisher proved that the distribution of ‘r’ is by no means normal and in the neighbourhood of ρ = ± 1, its probability curve is extremely skewed even for large n. if ρ ≠ 0, Fisher suggested the following transformation

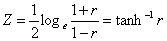
And proved that even for small samples, the distribution of Z is approximately normal with mean

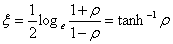
And variance 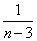and for large values of n, say > 50, the approximation is fairly good.

Email Based Homework Help in Exact Sampling Z Distribution

To submit Exact Sampling Z Distribution assignment click here.

Following are some of the topics in Exact Sampling Z Distribution in which we provide help: