Combination Of N Different Objects Assignment Help
Combination of n different objects:
i) The number of all combinations of n distinct objects taken r at a time is given by;
C(n, r) = n!/r! (n – r) !
Combination Of N Different Objects Assignment Help By Online Tutoring and Guided Sessions from AssignmentHelp.Net
where n! is a factorial.
Example: Evaluate C(10, 2)
Solution: Here,

n = 10
And r = 2
Using the general formula
C(n, r) = n!/ r! (n – r) !
we get
C(10, 2) = 10!/ 2! (10 – 2)!
= 10 x 9 x 8!/2! 8!
= 45
ii) C(n, n) = 1
Proof: we have,
C(n, r) = n!/ r! (n – r) !
putting r = n
C(n, r) = n!/ n! (n – n) !
= n!/ n! 0!
we know that
0! = 1
therefore,
C(n, n) = 1
iii) C(n, r) = C(n, n-r) for 0≤ r ≤ n
Proof: C(n, n-r) = n!/ (n – r) ! x [n – (n – r)] !
= n!/ (n – r) ! x (r) !
= C(n, r)
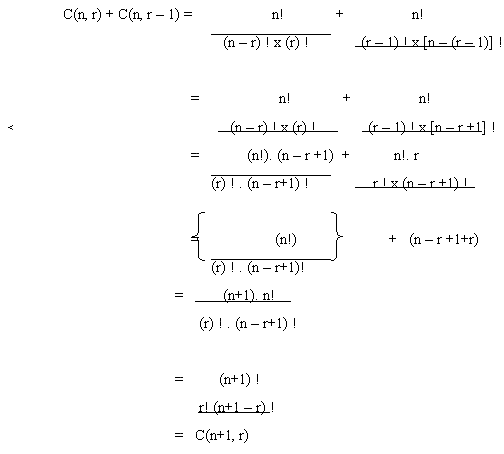
iv) C(n, r) + C(n, r – 1) = C(n+1, r)
Proof:
Email Based Assignment Help in Combination Of N Different Objects
To submit Combination Of N Different Objects assignment click here.