Definition of Annuity

Annuity refers to a regular cash flow which is received for a fixed period of time. (Denoted by A)

Annuity may occur at the end of each period or at the beginning of each period.

There are various ways to calculate the present value and the future value of an annuity as demonstrated below:

Present value of an end of the period annuity:

The present value of an annuity at the end of the period is calculated by discounting each cash flows to its present value and adding all these present values. It is denoted through a formula,

Present value of annuity =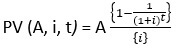

where, A = Annuity, i= Discount rate, t = Time period

Calculation of the Present Value of annuity occurring at end of the period

Example: ABC Limited is interested to invest in a property for $20,000 cash down payment or $5000 a year for 5 yearly payments for the same property. The opportunity cost is 10%. The ABC Limited should opt for which option?

Here the Present value of $5000 each year for the next five year can be found out using the present value of annuity formula

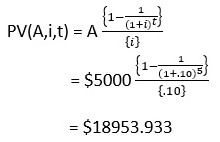
Learn now how to calculate present value

Since the present value of annuity payments is less than the cash down value, so it will be beneficial to pay through the annuity method. Annuity helps us to choose the right option among many options of payment.

Present Value of Multiple Annuities

The present value of multiple annuities is calculated by finding different present values of annuity individually year by year and summing them.

Example: Amon is an investment consultant in PY limited and trying to estimate the present value of the expected investment obligation.

{`
  Year        Amount
  1 - 5       $150 million
  6 - 10      $ 400 million
  11 - 20     $ 600 Million
  `}

Discounted Rate is 20%. Calculate present value of three Annuities

Solution for finding present value of multiple annuities

1) Present value of First Annuity

Present value of Second Annuity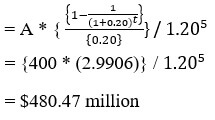

Present value of third Annuity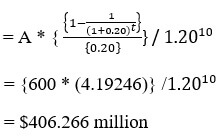

As per the solution it is clear that with the increase in the year the value of the investment increase. As the year increase the present value for the estimated year also increase.

Cumulative Present Value = $448.59 million + $480.47 million + $406.266 million = $1335.32 million

Amortization Factors and Finding Annuities Given Present Value

In this type of annuity, the present value is given and we have to calculate the estimated annuity value. This is related to the depreciation of a particular assets. This method is used with home vehicles and auto mobile loan sector. It is calculated through the following formula:

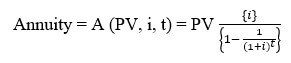
Let us consider how to calculate the value of an annuity when the present value is given through the following example

Suppose Remy wants to buy a car. He tries to borrow $200,000 on the conventional 20-year mortgage on semi-annually payment. The annual loan rate is 10%. The monthly payment is estimated as follows –

Semi-annually interest rate on loan = APR/ 2 = .10/2 = 0.05

Monthly Payment on mortgage =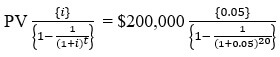

= $16,048.788

This means that that Remy will have to pay an annuity of $16,049 semi-annually to cover the present value mortgage of $200,000 in twenty years.

The monthly payment is an increasing function of interest rates.

Calculating the Future Value of End-Of-The-Period Annuities

In this case, the person plans to set aside the annuity amount in the starting for each period and will want to get the complete information that how much he will have at the end of the period. Thus what will be the future value of these annuities.

It is calculated through the formula given below

Future value of an annuity =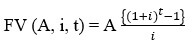

where, A= Annuity, i = Discount Rate, t = Number of year

Future Value of Annuity Calculations for Individual Retirement Accounts

Using Annuities for Calculations of IRA (Individual retirement accounts)

Mr Parks is a government employee. He sets aside amount of $5000 at the end of every year. He started from the age of 25 year, for an expected retirement at the age of 65 making an 10% return on its investment.

Calculate annuity on the following basis.

1) Non-tax deductible

Expected Future value of IRA set Aside for 40 years = = $221,262.77

2) Tax deductible @40%

Effective rate of return = [10% - (10%*40%)] = 6%

Future value of IRA set aside for 40 years = = $ 110,123.56
There is a deduction in amount through the loss of tax exemption.

Calculating Annuity Given Future Value

Individuals or businesses who have a fixed obligation to meet or a target to meet (in terms of funds) sometime in the future need to know how much they should set aside each period to reach this target. Basically it is the burden on the final amount payer in the form of interest

Annuity given future value = A (FV, i, t) =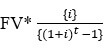

Calculation of annuity through its future value: example of sinking fund provision.

Sinking fund is the amount of interest which the person has to pay as an interest for its debt.

Consider XYZ limited issues bonds with a face value of $100 million coming due in 10 years. Then the annuity amount XYZ would need to set aside each year (assuming an interest rate of 8%):

$100,000,000* {.08}/( {(1+0.08)}¹⁰-1 ) = $6,902,950

Thus, XYZ would need to set aside $6.9 million at the end of each year to ensure that there are enough funds ($100 million) to retire the bonds at maturity.

Effect of Annuities at The Beginning Of Each Year

Annuity may be at the beginning of the period as well as at the end of the period. But usually the if the cash flow occur at the beginning of each period both present and future value is affected. This would not happen in the case of end of the period annuity.

Present value of beginning of the period annuity =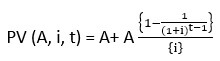

Future value of the beginning of the period annuity =

• This present value will be higher than the present value of an equivalent annuity at the end of each period.
• This future value will be higher than the future value of an equivalent annuity at the end of each period.

It is best to invest at the present value of annuity in the beginning of the period as gains will be larger.

Growing Annuities

As the name suggested it is basically the grow of the cash flow at the steady and constant rate for a specific period of time.

Assuming that the growth rate remains constant forever,
Growing annuity is calculated as below:

PV of a growing Annuity =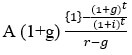

The above formula for calculating the present value of growing annuities work even when the growth rate of annuities is greater than the discount rate.

In case when the growth rate of the annuity is equal to the discount rate then annuity is calculated through = nA

Solved Example of Present Value of a growing annuity: Diamond Mine

TSTS limited has the rights to a Diamonds mine for the next 20 years, over which period they plan to extract 5,000 ounces of diamond every year. The current price per ounce is $300, but it is expected to increase 3% a year. The appropriate discount rate is 10%

Present value of diamonds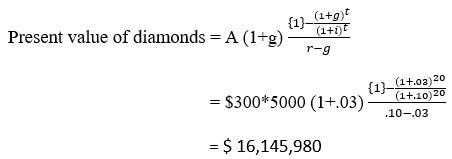

The present value of the Diamonds expected to be extracted from this mine is $16.146 million.

The present value of a growing annuity is an increasing function of the expected growth rate in Diamonds mines prices.

If the discounted rate increases with the same increase in the growth rate . The present value of the expected thing will decrease. It is because as the discount factor decreases it will decrease the present values.

Perpetuities

Perpetuity refers to a constant flow of income that lasts forever. It has a constant or a fixed rate of cash flow for a long period of time, as if forever at a regular interval.

The present value of perpetuity can be calculated by
PV of perpetuity = A/i
where A is Perpetuity

The future value of a perpetuity is infinite.

Example of a Present value of Perpetuity

A share issued 10% dividend with the interest rate of 5%. The present value of share would be 10/.05= $200

How to calculate the Present value of Growing Perpetuities

As the name suggested the growing perpetuities is the cash flow of the business expected to grow at a constant rate for an infinite period of time. The growth rate is at a fixed rate.

The present value of a perpetuity growing at a constant rate g, discounted at rate r and expected to yield a cash flow of CF1 next year is:

Present Value of growing perpetuity = CF₁/(r-g)

Growing annuity and the growing perpetuity have many common features. The basic difference is that the growing perpetuities are forever but the barrier is the growth rate. The growth rate of the perpetuity must be less than the discounted rate.

Let us understand the concept of growing perpetuity with the help of the example:

How to value a Stock with Stable Growth in Dividends

Suppose in 1992, American Express paid dividends per share of $5. Its earnings and dividends had grown at 10 % a year between 2000 and 2004 and were expected to grow at the same rate in the long term. The rate of return required by investors on stocks of equivalent risk was 15%.

{`
  Current Dividends per share = $5
  Expected Growth Rate in Earnings and Dividends = 10%
  Discount Rate = 15%
  Value of Stock = $5 *1.10 / (.15 -.10) = $11
  `}

As the value of the stock increase or decrease, it directly affects the growth rate in earnings and dividend. There is a direct relationship between value of stock and growth rate.

There is an inverse relationship between the interest rate and the present value of the bonds.

If the interest rate rises then the value (present value) of the bonds will Decrease. If the interest rate fall the present value of the bond will Increase.

In the case of bonds, the payments can be in combinations of annuities, perpetuities as well as simple cash flows. Thus in case of a bond that pays yearly coupon payments for n years as well as redeems for its face values at the end of n years, it represents the combination of annuity payments as well as simple cash flows.

The present value of this bond will be the sum of the present value of all annuity payments for n years as well as the present value of the face value cash flow.

There are two pricing proposition. They are as follows;

Bond Pricing Proposition 1: The longer the maturity of a bond, the more sensitive it is to changes in interest rates.

Bond Pricing Proposition 2: The lower the coupon rate on the bond, the more sensitive it is to changes in interest rates.

Incase of dividends on a stock, after a certain period of time the growth rate become stable and the value of the stock or bond start decreasing.

The dividend payments at first grow at a constant rate g for n years of high growth period. This represents payments as growing annuities. Post this, there is a stabke growth period in which the dividends continue to grow forever at a stable rate. This latter is a form of growing perpetuity.

Thus the value of this stock is a sum of two present values: growing Annuity and g rowing Perpetuity, discounted back

{`
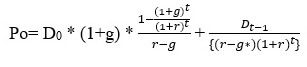
  where
  P0 = Present Value of dividends
  g = High growth rate for the first t years (t = High growth period)
  g* = Growth rate forever after year t
  D0 = Current dividends per share
  Dt = Dividends per share in year t
  i = Required rate of return at which the payments are discounted
  `}

Let us understand with the help of an Example on how to calculate the value of a stock dividend that has a high growth period for t years followed by a stable growth period forever.

Value of the stock growth

In 2010. Eda Barrack had earnings per share of $4.50 and paid dividends per share of $2.00. Analysts expected both to grow 9.81% a year for the next 5 years. After the fifth year, the growth rate was expected to drop to 6% a year forever, while the pay-out ratio was expected to increase to 67.44%. The required return on Eda barrack is 12.78%.

The price at the end of the high growth period can be estimated using the growing perpetuity formula:

{`
  Terminal price = DPS6 / (r – g*)
  = EPS6 * Payout Ratio in Stable Growth / (r – g*)
  = EPS0 (1+g)5 (1+g*) / (r – g*)
  = $ 4.50*1.09815*1.06*0.6744/ (.1278-.06) = $75.81
  `}

The present value of dividends and the terminal price can then be calculated as follows:

= $ 52.74

The value of Eda barrack stock, based on the expected growth rates and discount rate, is $52.74.

Online Finance Homework Help Tutors by Assignmenthelp.net

Looking for Expert finance tutors to help you understand concepts of finance such as present value of annuity, net present value, financial risk modelling, CAPM model, option pricing calculations and more? Assignmenthelp.net is the best place to hire online finance tutors who are reliable as well as affordable. All our finance tutors are leading experts in their fields and have studied core finance topics in their graduate schools and business schools. Our online finance tutors are rigorously tested for providing correct, academically sound and detailed step-wise solutions to help students complete their finance homework assignments. We have online finance tutors from leading business schools and graduate schools in the world who are equipped to help students in theoretical finance courses, financial modelling in excel and VBA as well as conduct financial analysis and even valuations based on DCF models and CAPM, LBO and more. If you are looking for cheapest finance tutors in US, UK, Australia, UAE or are just looking to hire the best finance tutor in Canada then hire them now on www.assignmenthelp.net and get the best affordable online homework help in finance.