Physics Assignment Help With RC-Circuits

1. Home
2. Physics
3. DC Circuit
4. RC-Circuits

11.11 RC-Circuits

11.11.1 Charging of Capacitor

The figure shows a circuit arrangement in which a capacitor in series with a resistor is connected across a battery of emf E through a switch S.

When the switch S is closed the current starts flowing and the capacitor starts charging. If I be the instantaneous charge on the capacitor, then applying Kirchoff’s Voltage Law.



Since I = , the above equations may be rearranged as

RC = CE - q

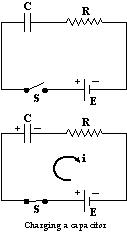
or

After integrating we get

ln |CE - q| =

At t = 0, q, = 0 Þ K = ln |CE|

\ q = CE ( 1 - e-t/RC)

The instantaneous potential difference across the capacitor is

v =

The instantaneous current through the circuit is

i =

The graphs showing the variation of q, v and i with time are shown as below.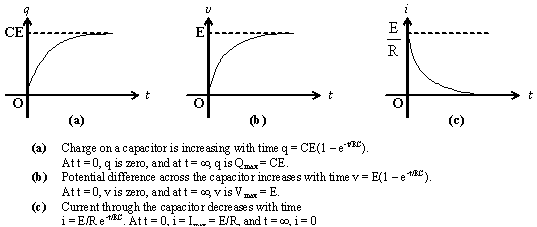



The charging of a capacitor may be summarised as

q = Qmax (1 - e-t/t)

v = Vmax (1 - e-t/t)

i = Imax e-t/t

Where Qmax = CE; Vmax = E; Imax =E/R and t = RC (time constant)

The time constant t is defined as the time during which charge on the capacitor rises to 0.63 times the maximum value.

Mathematically,

when t = t, q = qmax (1-e-1)

or q = 0.63 qmax

Email Based Assignment Help in RC-Circuits

We are the leading online Assignment Help provider. Find answers to all of your doubts regarding the RC-Circuits. Assignmenthelp.net provide homework, Assignment Help to the school, college or university level students. Our expert online tutors are available to help you in RC-Circuits. Our service is focused on: time delivery, superior quality, creativity and originality.

Following are some of the areas in physics DC Circuit which we provide help: