Traveling Salesman Problem using Genetic Algorithm Sample Assignment

Travelling Salesman Problem using Genetic Algorithm

Executive summary

The Travelling Salesman Problem is to find the best path for a salesman who intends to travel n number of cities. Cost of traversing this path is directly proportional to the distance covered. The distance matrix depicting the value between any two cities is chosen at random. Further on rank based strategy, the elite combination is made to mutate and they must produce further fittest surviving combinations. The best result on performing mutation and crossover is outputted as result. This report shows the results obtained after multiple runs using different mutation techniques and draw analysis to identify which set of technical approach brings better results in least amount of time.

Choice of approaches:

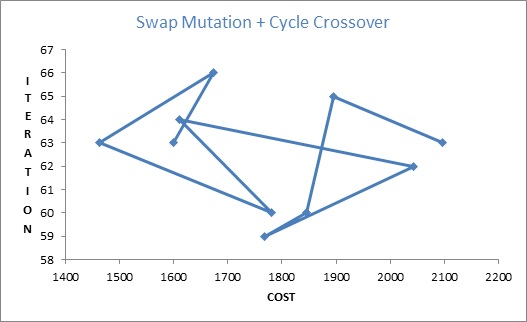
Approach I: Rank-based selection (Elitism) + Swap mutation + Cycle Crossover

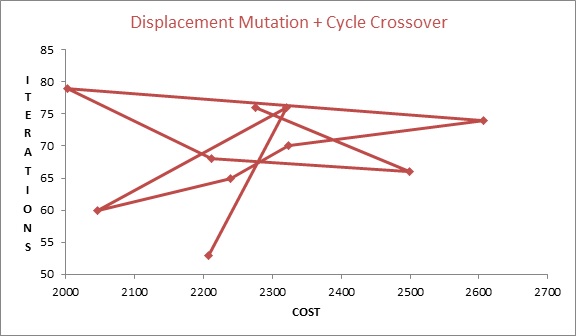
Approach II: Rank-based selection + Displacement mutation + Cycle Crossover

List of assumption made in code

1. Number of cities that the salesman has to travel is 50. Though this value can be modified as per user choice.
2. Distance between any two cities is set maximum to be 100. This is done to restrain computation time. When exact distance matrix will be used, need for setting an upper bound can be eliminated.
3. All the cities are represented by integral values from 1 to 50.
4. A maximum of 50 generations are looked to get the best results. This acts as termination condition for the algorithm.

Analysis:

Analysis will be done in 2 parts:    1. Compare two GA strategies as decided.

2. Compare result from GA and local search technique.

The source code is run 10 times. Following data is recorded in Table 1.

1. Time taken by each algorithms and
2. Number of iterations occurred
3. Cost for traversing the best path

Table 1

Observations

1. The best cost for Set I (Swap mutation + cycle crossover) is 1463 during 8^th Result computed in 7 milliseconds using 63 iterations.
2. Best cost for Set II (Displacement mutation + cycle crossover) is 2003 during 4^th Result computed in 16 milliseconds and 79 iterations.
3. Average cost for Set I is 1777.4 and for Set II is 2273.3
4. Average time for Set I result is 5.1 milliseconds and for Set II is 15.6 milliseconds
5. Average number of iterations made to reach results in case for Set I is 62.5 and in case for Set II is 68.7

Inferences based on observation:

1. In current problem scenario: Swap mutation + cycle crossover has yield better results with respect to time, cost values and number of iterations as compared to Second approach which uses - Displacement mutation + cycle crossover.
2. In spite of consuming more time and going through more iteration displacement mutation does not yield results as good as Swap mutation.

Graph 1 shows below support the inferences made:

Graph 2

Performance evaluation

The TSP problem under current scenario is symmetric. This implies that the cost to reach point B from A and point A from B is same. For an example involving only 3 cities say 1, 2 and 3. It is easy to compute the best path among [1, 2, 3] and [1, 3, 2] believing the salesman starts from city 1. But with increasing number of cities, these calculations of possible permutations will become complex, exhaustive and time consuming. The Genetic Algorithm approach aims to solve this issue. Evaluation has been made on the basis of performance displayed by these algorithms using an Intel core i3 processor system with respect to time, memory used and quality of solution obtained.

1. TSP is an NP-hard problem in combinatorial optimization. That implies by local search algorithm, the complexity of solution is O(n!) where n represent number of cities.
2. The complexity for Rank based selection to identify the fittest individual is O(n).
3. The complexity for Cycle crossover operation is also O(n). Suppose the algorithm is run for m number of generation then the complexity becomes O(mn).
4. For swap mutation, time complexity of running the algorithm is O(1) as the swap is made at an index randomly chosen.
5. For displacement mutation, a subset of path is chosen and re-located, the complexity of algorithm depends on the length of the subset say L and total number of cities say N. The complexity becomes O (^NC_L) x O (N-L+1).

Table 2:

Table 3:

Calculates complexity values for each solution technique

- Varying number of cities,

- Length of ‘l’ is set to be (n-2),

- Value of ‘m’ is maxed out to be 100.

Conclusion

Based on the calculations above, it is clear that with increasing number of cities, swap mutation + cycle crossover will give cost values faster as compared to second GA approach or local search. Difference between complexities of algorithm is huge and suggests use of evolutionary genetic algorithm in real world computation where the geographical space is diverse and areas are divided into many cities. Using dynamic programming after a certain value of n will consume lot of space and time to yield results.

However, the GA algorithm may get stuck at local minima values. To avoid such situations , value of m and l must be changed accordingly and algorithm should be run multiple times before reaching to a result in real life applications. The aim must be to move as close to global minima as possible.