Titanic Survivability Prediction Sample Assignment

Titanic Survivability Prediction

Introduction

The Titanic tragedy was one of the most devastating and deadliest events that ever happened in modern history. Prediction models have been developed to estimate the probability of survival among the passengers in the liner, in consideration to factors such as className, gender and age among others. Lots of machine learning activities and predictive methods have been tried to develop a model with the highest predictive power of survivability in the incident.

1. Defining Business Objectives

This paper is focused on developing a predictive model to predict the probability that an individual would have survived the accident given different factors, which affected the victims differently. The passenger liner was divided into 3 classes –first className being in the topmost, second className in the middle and third className being at the bottom. This already shows that people in the third className were more likely to die compared to the other classes. However, it is important to prove this hypothesis, hence supporting our ideas and theories.

It has been documented that most people die because there were no enough lifesaving jackets, which rendered most of the people who could have survived death. Due to theories of nature, scarcity of the lifesaver jackets exposed men more compared to the other groups – women and children. In addition, this effect would have been affected by levels of className. It would be hypothesized that men in the first className were more romantic compared to those in second and third classes. Therefore, the trends of survivability would vary between className for men and women. In an ideal situation, men and women in the third className would have struggled in the same manner to save their lives.

It is possible to predict their survivability based on the dynamic structure of the catastrophe. As much as the survivability levels would have been due to chance, these dynamics can explain to some level of confidence. Exploratory data analysis will be conducted to identify the predictive variables for survivability. Therefore, a model will be developed to explain the probability of survival using the provided variables explained in the metadata below.

Methods

2. Preparing Data

Survival, ticket className and port of embarkation were recorded as categorical variables using the factor() function for ease of analysis. Using the number of siblings and the number of parents, family size was calculated. Also, a large family was defined as which has more than three individuals. Extraction of individuals’ titles was done to generate other categorical variables which would possibly contribute in the model development. For instance, men were differentiated from male kids by extracting ‘Mr.’ titles. Subsets of the data were created to effectively analyse the data for insights into the model development stage.

Table 1: Data dictionary

3. Exploratory Data Analysis

According to our data set, 62.3% died and 37.7% survived. Among the males, 87.1% died while 17.4% died among the females. On average, those who survived had paid double as much fare as the survivors.

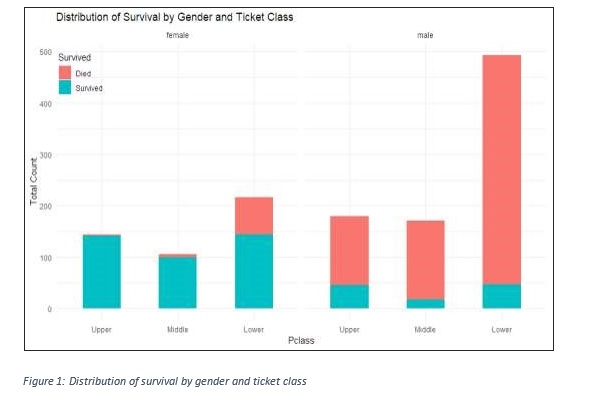
According to the figure below, a higher proportion of males died as compared to the females. More males in the middle and lower classes died as compared to those in the upper className. Amongst the females, the survival rate among those in the lower className was smaller compared to those in the upper and middle-className category (Jordan and Kleinberg, 2006).

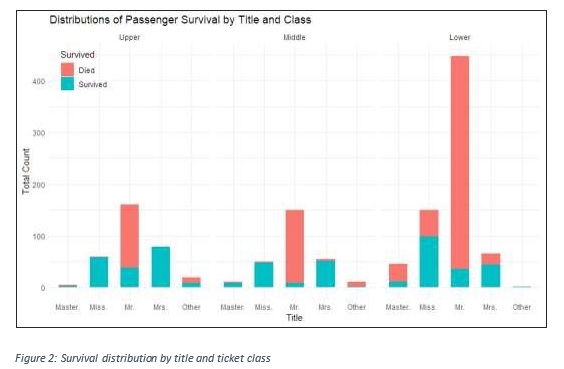
As shown in the figure below, few passengers who had “miss” and “Mrs” titles died in upper className compared to middle and lower className categories.

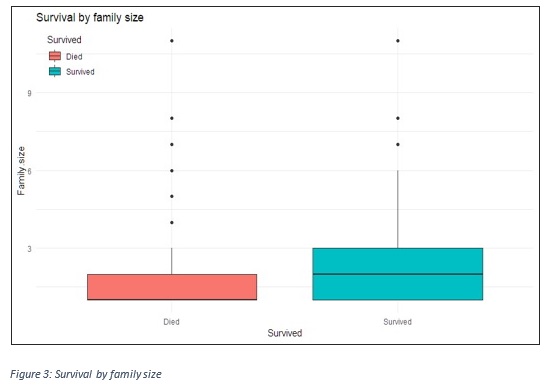
On average, the survivors had larger families. Some extreme values are observed, indicating that few individuals had more than family members on board.

More male died in all the classes than females and the proportions of females who died in the three className reduce significantly from third className to first className.

4. Data Sampling

Using the caret’s package function, createDataPartition (), the train and test datasets were created a 70 to 30 ratio respectively.

set.seed(999)

train.samples <- createDataPartition(y = TitanicData$Survived, p = .70,list = FALSE)

train <- TitanicData[train.samples, ] test <- TitanicData[-train.samples, ]

5. The Logistic Model

According to the data exploration performed in this paper, the best model includes ticket className, sex, age, passengers with “Mr.” initials and family size. The model output is shown in the table below.

## glm(formula = Survived ~ Pclass + Sex + Age + Mr + Family.size,

## family = "binomial", data = train)

##

## Deviance Residuals:

## Min 1Q Median 3Q Max

## -2.4310 -0.5103 -0.3149 0.5270 2.6117

##

## Coefficients:

## Estimate Std. Error z value Pr(>|z|)

## (Intercept) 4.615628 0.527027 8.758 < 2e-16 ***

## PclassMiddle -1.559324 0.317087 -4.918 8.76e-07 ***

## PclassLower -2.433104 0.317273 -7.669 1.74e-14 ***

## Sexmale -2.337843 0.388411 -6.019 1.76e-09 ***

## Age -0.033125 0.008768 -3.778 0.000158 ***

## Mr -1.509350 0.403529 -3.740 0.000184 ***

## Family.size -0.221536 0.081176 -2.729 0.006351 **

## ---

## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

##

## (Dispersion parameter for binomial family taken to be 1)

##

## Null deviance: 987.05 on 731 degrees of freedom

## Residual deviance: 550.91 on 725 degrees of freedom

## (185 observations deleted due to missingness)

## AIC: 564.91

##

OR 2.5 % 97.5 %

## (Intercept) 101.05126328 37.12359554 293.8110424

## PclassMiddle 0.21027808 0.11159168 0.3876449

## PclassLower 0.08776403 0.04631873 0.1610626

## Sexmale 0.09653569 0.04421031 0.2039411

## Age 0.96741808 0.95063377 0.9839373

## Mr 0.22105368 0.10026833 0.4913842

## Family.size 0.80128703 0.68099737 0.9369452

All the variables included in the model are statistically significant with 95% confidence level (Elliott and Woodward, 2007; McCluskey and Lalkhen, 2007; Ledolter, 2013).

The table above includes exponents of the coefficient in the model, which indicate that all the predictor variables were associated with lower odds of survival. Individuals in the middle className were less likely to survive by 21.03% compared to those in the first className keeping the other factors constant. Similarly, those in the lower className were less likely to survive by 91% compared to those in the upper-className category. Male individuals in the passenger liner were less likely to survive by approximately 90%, by controlling for the other variables in the model. Increasing age by 1 year reduces the odds of surviving by around approximately 3%. Males with “Mr.” initials in their names were less likely to survive by approximately 78% after controlling for the other variables in the model. Finally, increasing family size by one member led to approximately 20% reduced chance of survival (Hosmer, Lemeshow and Sturdivant, 2013; Ledolter, 2013).

6. Model Validation

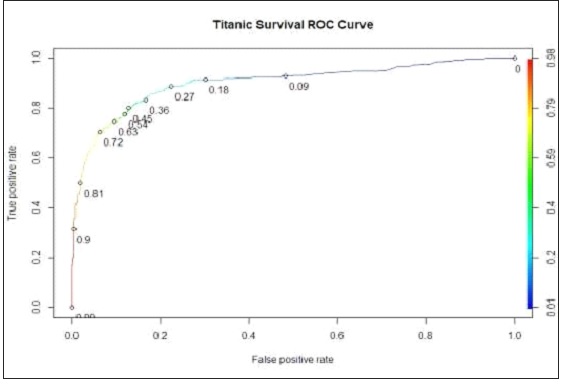
Figure 4: Model ROC plot

According to the ROC plot shown above, the best threshold to be used in the prediction will be 0.54. The area under the curve is approximately 90.29%, showing that the model is very good.

7. Model Prediction table(test$Pred_Survived)

prop.table(table(test$Pred_Survived))

table(test$Pred_Survived, test$Sex)

prop.table(table(test$Pred_Survived, test$Sex),2)

table(test$Pred_Survived, test$Pclass)

table(test$Pred_Survived, test$Survived)

prop.table(table(test$Pred_Survived, test$Survived), 2)

33.63% (112) were predicted to have survived in the test dataset and 66.37% (221) to have died. Of those who survived, 16% (18) were men and 84% (94) were women. 15% of the survivors were from the third className, 26.6% from second className and 56.25% from first className (Michael, 2001; Sainani, 2013).

Conclusion

In conclusion, gender, age, ticket className, family size and having a “Mr” initial effectively predicts the probability of survival using the Titanic data set. The model's overall accuracy is 90.29%, indicating that it can accurately classify survival and deaths 90% of the times per 100 persons. According to the ROC curve, we can conclude that the best threshold to predict survival is around 0.54. Using this threshold, the model has a sensitivity of 77.8% and specificity of

94.27%.

References

Elliott, A. C. and Woodward, W. a. (2007) ‘Analysis of Categorical Data’, Statistical Analysis Quick Reference Guidebook, pp. 113–150. doi: 10.1007/SpringerReference_60770.

Hosmer, D., Lemeshow, S. and Sturdivant, R. X. (2013) ‘Model-Building Strategies and

Methods for Logistic Regression’, in Applied Logistic Regression, pp. 89–151. doi:

10.1002/0471722146.ch4.

Jordan, M. and Kleinberg, J. (2006) ‘Information Science and Statistics’, Pattern Recognition, 4(356), pp. 791–799. doi: 10.1641/B580519.

Ledolter, J. (2013) Data Mining and Business Analytics with R, Data Mining and Business Analytics with R. doi: 10.1002/9781118596289.

McCluskey, A. and Lalkhen, A. G. (2007) ‘Statistics III: Probability and statistical tests’, Continuing Education in Anaesthesia, Critical Care and Pain, 7(5), pp. 167–170. doi:

10.1093/bjaceaccp/mkm028.

Michael, R. S. (2001) ‘Crosstabulation and Chi-square’, Indiana University Retrieved, pp. 1–8.

Sainani, K. L. (2013) ‘Understanding linear regression’, PM and R, 5(12), pp. 1063–1068. doi:

10.1016/j.pmrj.2013.10.002.