Systems Of Linear Equations Assignment Help

Introduction to the System of linear equation

A linear equation in variables x1, x2, x3, xn is an equation of form a1 x1+ a2 x2+........... + anxn =b

Where a1, a2, a3................an and b are constant real or complex number. A system of linear equations is a finite collection of linear equations involving the same set of variables.

For example,

3x+2y-z=1

2x-2y+4z=-2

-x+1/2y-z=0

Solution: x=1,

y=-2

z=-2

General form for system of linear equations:

Vector equation: One extremely helpful view is that each unknown is a weight for a column vector in a linear combination.

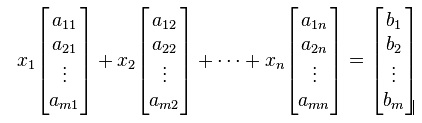
Matrix equation: The vector equation is equivalent to a matrix equation of the form

Ax = b

Where A is an mn matrix, x is a column vector with n entries and b is a column vector with m entries.

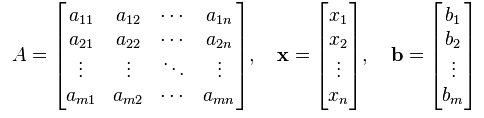
The number of vectors in a basis for the span is now expressed as the rank of the matrix.

Properties of System of linear Equation:

• Independence
• Consistency
• Equivalence

The four expressions of a linear system:

1.A general system of linear equations can be written a

a11x1 + a12x2 + ...... + a1nxn = b1

a21x1 + a22x2 + ......... + a2nxn = b1

am1x1 + am2x2 + ...... + amnxn = bm

The vector equation form: x1a1 + x2a2 + + xnan = b;

3. The matrix equation form: Ax = b

4. The augmented matrix form: [a1, a2......., an | b]

Several algorithms for solving a linear equation:

• Describing the solution
• Elimination of variables
• Row reduction
• Cramer's rule
• Matrix solution
• Other methods