Set of Complex Numbers

We know that the solution of the quadratic equation

ax² + bx + c = 0, a≠0

are given by quadratic formula

x = -b ± √(b²-4ac)/2a

Now when b²-4ac < 0 the equation cannot be solved in real number system. For this solution, we need the set of complex numbers.

i= √(-1)

The set of complex numbers denoted by ℂ is defined as:

{`ℂ = {a+bi∶a,b ∈ R,i = √(-1)}`}

The notation a + bi is called writing complex number in standard form

a is called the real part of complex number z= a + bi (also written as a = Re z) and b is called the imaginary part of complex number z = a+bi (also written as b = Im z ).

Complex Number Examples

Examples of complex numbers can be given as 2+4i or √(-9 )=9i etc.

Two complex numbers z₁= a₁+b₁ i and z₂= a₂+ b₂ i are equal if their real and imaginary parts are equal, which means a₁=a₂ and b₁= b₂.

Every real number is a complex number with its imaginary part 0. Thus a = a + 0i

So R ⊂ ℂ

Conjugate of a Complex Number

The complex number z̅= a - bi is called the conjugate of a complex number z = a + bi .

Absolute Value of Complex Numbers

The absolute value of complex number z is defined as |z|= √(a²+b²)

Operations with Complex Numbers

Two complex numbers can be added, subtracted, multiplied and divided resulting in new complex numbers.

If z₁= a₁ + b₁ i and z₂ = a₂ + b₂ i then

Adding Complex Numbers

z₁ + z₂ = (a₁ + a₂ ) + (b₁ + b₂ )i

Subtracting Complex Numbers

z₁ - z₂ = (a₁ - a₂ )+(b_1-b_2 )i

Multiplying Complex Numbers

z₁ z₂ = (a₁ a₂ - b₁ b₂ )+(a₁ b₂ + a₂ b₁ )i

Dividing Complex Numbers

z₁/z₂ = a₁ + b₁ i/a₂ + b₂ i = (a₁ + b₁ i)( a₂ - b₂ i) )/(a₂ + b₂ i)(a₂- b₂ i) = (a₁ a₂+ b₁ b₂)/(a₂² + b₂² ) - (a₁ b₂ + a₂ b₁)/(a₂² + b₂² ) i

Then,

1/z= 1/(a+bi)= (a-bi)/((a+bi)(a-bi)) = (a-bi)/(a²+b² )= a/(a^2+b2 ) - b/(a²+b² ) i

Simplifying Complex Numbers

For simplifying complex numbers we must remember the various powers of imaginary number I, especially while multiplying imaginary numbers:

• i² = 1 ,
• i³ = -i ,
• i⁴ = 1 ,
• i⁵ = i ,
• i⁶ = -1 ,
• i⁷ = -i…

Properties of Complex Numbers

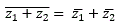1. or the conjugate of the sum of complex numbers is the sum of the conjugates of complex number
2. z̅₁̅z̅₂̅ = z̅₁.z̅₂ or the conjugate of the product of complex numbers is the product of the conjugates of complex number
3. z̅. z = |z|² or the product of the complex number with it’s own conjugate is equal to the square of the absolute value of that complex number
4. z̅ + z = 2 Re z or the addition of a complex number with its own conjugate is equal to twice the real part of the complex number
5. z - z̅ =2i Im z or subtracting the conjugate of a complex number from the complex number is equal to two times iota multiplied by the imaginary part of the complex number
6. Re z ≤ |z| or the real part of the complex number is less than or equal to the absolute value of complex number
7. z̿ = z or the conjugate of a conjugate of complex number is the complex number itself.
8. z is real if and only if z̅ = z or if the conjugate of a complex number is equal to the complex number itself then the complex number is a real number, that is it has only a real part and no imaginary part.

Solved Example for Complex Number Properties and Operations with Complex Numbers

Let z₁ = 3 - 2i and z₂ = -2 + 3i then

Re z₁ = 3, Im z₁ = -2 and

Re z₂ = -2, Im z₂ = 3

|z₁ | = √(3² + (-2)² ) = √13

|z₂ | = √((-2)²+ 3² )= √13

z₁ + z₂ = (3-2)+(-2+3)i = 1+i

z₁ -z₂ = (3 -( -2)) + (-2 -3)i = 5-5i

z₁ z₂ = (3*(-2)-(-2*3))+(3*3+(-2*-2))i = 13i

z₁/z₂ = 3-2i/-2+ 3i = 3*(-2) + (-2*3)/4+9 - 3*3 +(-2 * -2))/4+9 i = -12/13 + 13/13 i= -12/13 + i

1/z₁ = 1/3-2i = 3/13 + 2/13 i

1/z₂ = 1/-2+3i = -2/13 - 3/13 i

z̅₁ =3 +2i

z̅₂ = -2 -3i

z̅₁ + z̅₂ = (3 - 2)+(2 - 3)i = 1-i

Hence verified: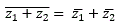

z̅₁ . z̅₂ = (3*(-2)-(-2*3)) + (3*-3+(2*-2))i = -13i

z̅₁̅z̅₂̅ = 1̅3̅i = - 13i

Hence verified: z̅₁̅z̅₂̅ = z̅₁ . z̅₂

z̅₁.z₁ = (3-2i)*(3+2i)=(9+4)+(-2*3+3*2)i=13=(√13)² = |z₁ |²

Hence verified: z̅.z = |z|²

z̅₁ + z₁ = (3-2i)+(3+2i)= 6 = 2*3 = 2Re z₁

Hence verified: z+z̅ = 2 Re z

z₁ - z₁̅ =(3-2i) - (3+2i) = -4i = 2i(-2) = 2i Im z₁

Hence verified: z-z̅ = 2i Im z

Hence verified: Re z ≤ |z|

z̿₁ = 3̿-̿2̿i̿ = (3+2i) ̅ = 3-2i = z₁

Hence verified: z̿ = z

Applications of Complex Numbers

Complex numbers have vast applications in the field of electrical engineering, study of electrical circuits, trigonometry, calculus, quantum mechanics, and study of waves such as electricity, light, and sound. Or simply in finding square root of negative numbers.

Want to know more about complex numbers? Order our Math Homework Help service to increase your knowledge about complex numbers. Our Online Math tutors can help you with anything from operations on complex numbers to properties of complex numbers and even teach application of complex numbers to areas like Quantum physics, economics, electrical engineering and more. So Hurry, Order Math Help Now !