Real numbers and Irrational Numbers Assignment Help

Introduction to the Real number

Real number: A real number is a value that represents a quantity along a continuous line. The real numbers include number we normally use, such as 1, 15.82, -0.1, 3/4, etcPositive or negative, large or small, whole numbers or decimal numbers are called Real Numbers.

Properties of Real Numbers:

Let a, b, and c represents real numbers.

• Closure properties of Addition; a = b is a real number.
• Closure propertied of multiplication; ab is a real number.
• Commutative property of Addition; a + b = b + a.
• Commutative Property of Multiplication; a.b = b.a
• Associative Property of Addition; (a + b) + c = a = ( b + c)
• Associative Property of Multiplication; (ab)c = a(bc)
• Distributive Properties; a(b +c )= ab+ ac
  (a + b)c =ac + bc
• Multiplicative Identity Property a.1 = 1.a = a

Irrational Number

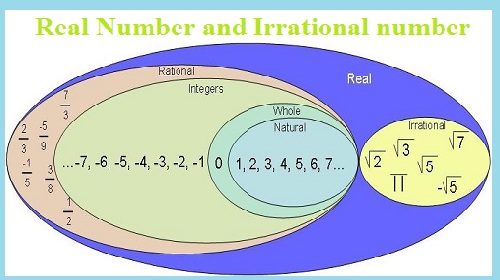
Irrational number is any number which cant be expressed as the ratio of integers. This type of real number cannot represented as repeating decimals or terminating. Example for irrational number: Euler's number e, the golden ratio , he ratio of a circle's circumference to its diameter .

Example: We prove that 2 is irrational. Assume to the contrary that (2 ) is rational, that is 2 =P/q

Where p and q are integers and q 0. Moreover, let p and q have no common divisor > 1. Then

2=p2/q2 2q²=p² (1)

Since 2q² is even, it follows that p² is even. Then p is also even (in fact, if p is odd, then p² Is odd). This means that there exists k Z such that

p=2k (2)

Substituting (2) into (1), we get

2q² = (2k)² 2q² = 4k² q²=2 = 2k²

Since 2k² is even, it follows that q² is even. Then q is also even. This is a contradiction.