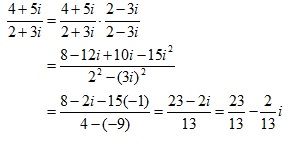Radicals Assignment Help

Radicals Introduction
An equation that contains roots involving variables, such as (x-5) =2 is called a radical equation. The main goal in solving them is to get rid of roots and to convert the radical equation to some simple, known equation.
Product rule for radicals:
na . nb = nab
Quotient rule for radicals:
na / nb = na/b

Adding and Subtracting Radical Expressions:
We can add or subtract radicals using the distributive property.
Example: 53 +23
= (5+2)3
= 73
Multiplying Radical Expressions:
Using special product rule with radicals:
(a-b) .(a+b) = a2 +b2
Solving an equation with radicals:
- Isolate the radical (or at least one of the radicals if there are more than one).
- Square both sides
- Combine like terms
- Repeat steps 1-3 until no radicals are remaining
- Solve the equation
- Check all solutions with the original equation (some may not work)
Example
x= (3x+7) -1
Adding 1on both side x+1 = (3x+7)
Squaring both side x2+2x+1=3x+7
Subtracting 3x+7 from both side:
x2 + x-6=0
(x-3)(x+2) =0
So x = -2 and x = 3, but only x =3 makes the original equation equal.
Dividing by a complex number: