PETE 2060 Assignment
Project 2: Flow in a 1-D reservoir
Consider slight compressible flow in undersaturated reservoir (i.e. pressure remains above bubble point) with a dip of 3° and wells represented as mass source/sink. Following governing equation describes such flow in porous media:
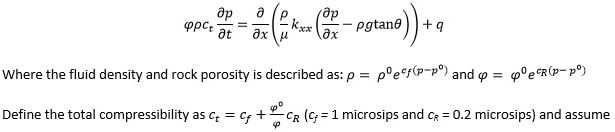
that fluid viscosity is constant (= 3 cp) for your problem. All boundaries are no flow (i.e. set transmissibility coefficient to zero). Each grid block has the dimension of 100 ft X 100 ft (assume no variation in the third direction). Initial reservoir pressure MUST be hydrostatic with the first gridblock pressure set as the datum value of 3000 psia. Reference fluid density and rock porosity evaluated at 3000 psia are 0.85 SG and 0.15.
X: Injector Well, ●: Producer Well -- Apply the specified flow rate (at reservoir condition – to avoid using FVF) for injector well as 2000 res. Bbl/day and use the average drawdown of 100 psia for the producer well.
HINT: Convert into consistent units before you discretize the terms in governing equation.
|
P1 10 mD 0.15 |
P2 5 mD 0.15 |
P3 10 mD 0.15 X |
P4 20 mD 0.15 |
P5 25 mD 0.15 |
P6 15 mD 0.15 |
P7 10 mD 0.15 |
P8 10 mD 0.15 ● |
P9 15 mD 0.15 |
P10 5 mD 0.15 |
Task 1: Write a linear algebraic solver for N X N system for the gridblock pressures as unknowns.
Task 2: Determine the transmissibility coefficients for your system and solve it. Present the results (i.e. pressure distribution in the reservoir) at three different time instances of 10, 30, and 90 days by solving the system of equations using time steps of 1, 2, and 3 days respectively.


