MGMT 2012 Introduction to Quantitative Methods

Question 1 A

CWD Investments, is a brokerage firm that specializes in investment portfolios designed to meet the specific risk tolerances of its clients. A client who contacted CWD this past week has a maximum of $50,000 to invest. CWD’s investment advisor decides to recommend a portfolio consisting of two investment funds: an Internet fund and a Blue Chip fund. The Internet fund has a projected annual return of 12%, whereas the Blue Chip fund has a projected annual return of 9%. The investment advisor requires that at most $35,000 of the client’s funds should be invested in the Internet fund. CWD services include a risk rating for each investment alternative.

The Internet fund, which is the more risky of the two investment alternatives, has a risk rating of 6 per thousand dollars invested. The Blue Chip fund has a risk rating of 4 per thousand dollars invested. For example, if $10,000 is invested in each of the two investment funds, CWD’s risk rating for the portfolio would be 6(10) +4(10)= 100. Finally, CWD developed a questionnaire to measure each client’s risk tolerance. Based on the responses, each client is classified as a conservative, moderate, or aggressive investor. Suppose that the questionnaire results classified the current client as a moderate investor. CWD recommends that a client who is a moderate investor limit his or her portfolio to a maximum risk rating of 240.

1. Formulate a linear programming model that can be used to determine the recommended investment portfolio to maximize annual return.(5 marks)b. Graph the feasible region.(4 marks)
2. Determine the coordinates of each extreme point.(3 marks)
3. Solve for the maximum return.(3 marks)
4. Solve in excel using the template provided. (5 marks)

Question 1 B

Salsa Inc., produces various Mexican food products and sells them to Western Foods, a chain of grocery stores located in Texas and New Mexico. Salsa Inc., makes two salsa products: Western Foods Salsa and Mexico City Salsa. Essentially, the two products have different blends of whole tomatoes, tomato sauce, and tomato paste. The Western Foods Salsa is a blend of 50% whole tomatoes, 30% tomato sauce, and 20% tomato paste. The Mexico City Salsa, which has a thicker and chunkier consistency, consists of 70% whole tomatoes, 10% tomato sauce, and 20% tomato paste. Each jar of salsa produced weighs 10 ounces. For the current production period, Salsa Inc. can purchase up to 280 pounds of whole tomatoes, 130 pounds of tomato sauce, and 100 pounds of tomato paste; the price per pound for these ingredients is $0.96, $0.64, and $0.56, respectively. The cost of the spices and the other ingredients is approximately $0.10 per jar. Salsa, Inc. buys empty glass jars for $0.02 each, and labelling and filling costs are estimated to be $0.03 for each jar of salsa produced. Salsa’s contract with Western Foods results in sales revenue of $1.64 for each jar of Western Foods Salsa and $1.93 for each jar of Mexico City Salsa.

1. Develop a linear programming model that will enable Salsa Inc. to determine the mix of Salsa products that will maximize the total profit contribution. (15 marks) Hint: convert to ounces to formulate the constraint. Find unit cost per jar and subtract from revenue to get net

profit per jar. Hint: The cost per jar of tomato in western food is .96/16*10*0.5=0.30

1. Solve in Excel using the Template provided (5 marks)

Question 1 C

CWD Agro Inc. produces two pepper sauces, Spicy Diablo and Red Baron. These sauces are both made by blending two ingredients, A and B. A certain level of flexibility is permitted in the formulae for these products. The allowable percentages, along with revenue and cost data, are given in the following table. Up to 80 quarts of A and 60 quarts of B could be purchased. CWD can sell as much of these sauces as it produces.

Formulate an LP whose objective is to maximise the net profit from the sale of the sauces. 20 marks

Question 2

Digital Controls, Inc. (DCI) manufactures two models of a radar gun used by police to monitor the speed of automobiles. Model A has an accuracy of plus or minus 1 mile per hour, whereas the smaller model B has an accuracy of plus or minus 3 miles per hour. For the next week, the company has orders for 100 units of model A and 150 units of model B.

Although DCI purchases all the electronic components used in both models, the plastic cases for both models are manufactured at a DCI plant in Newark, New Jersey. Each model A case requires 4 minutes of injection-moulding time and 6 minutes of assembly time. Each model B case requires 3 minutes of injection-molding time and 8 minutes of assembly time. For next week, the Newark plant has 600 minutes of injection-molding time available and 1080 minutes of assembly time available. The manufacturing cost is $10 per case for model A and $6 per case for model B.

Depending upon demand and the time available at the Newark plant, DCI occasionally purchases cases for one or both models from an outside supplier in order to fill customer orders that could not be filled otherwise.

The purchase cost is $14 for each model A case and $9 for each model B case. Management wants to develop a minimum cost plan that will determine how many cases of each model should

be produced at the Newark plant and how many cases of each model should be purchased. The following decision variables were used to formulate a linear programming model for this problem:

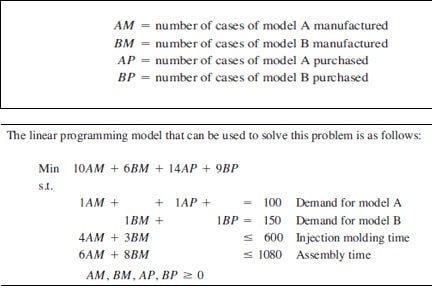
Answer the following questions (a-i) using the output below please be brief. If there are two possible answers one will suffice. Where necessary a range analysis must be shown.

1. What is the optimal solution (in words? (2 marks)

1. Twenty five (25) hours of molding were lost due to machine breakdown. Evaluate the effect? Explain- ( 3 marks)
2. An additional twenty hours of assembly time became available. Evaluate the effect? (3 marks)
3. Demand for model A increases by 10. Evaluate the effect (3 -marks
4. Suppose the purchase cost per unit for B (BP) decreased by $2. Evaluate the effect (3 marks)

11. Suppose that the manufacturing cost increases to $11.20 per case for model A (AM).

What is the new optimal solution? 2 marks

11. Suppose that the manufacturing cost increases to $11.20 per case for model A and the manufacturing cost for model BM decreases to $5 per unit. Would the optimal solution change (use 100 percent rule) 3 marks
12. Is the problem degenerate? Explain! (2 marks)
13. Are there alternative optima in this problem? Explain (2 marks)

Microsoft Excel 14.0 Answer Report

Worksheet: [Assignment 2 S2 2014-15 solutionB.xlsx]Q1B LP formulation MAX

Objective Cell (Min)

Variable Cells

Constraints

Microsoft Excel 14.0 Sensitivity Report

Variable Cells

Constraints

Question 3 A

Passengers arriving at a suburban rail ticket office during the morning peak commuter period frequently have to wait for service. There is one clerk who issues tickets and provides an information service for passengers. The manager has received complaints regarding the time passengers spend in the queue waiting to be served, and she wishes to investigate possible methods of reducing the queueing time. Possible ideas include employing a second ticket clerk who could either share the work of the existing clerk or perhaps handle enquiries only. Another idea may be to collect fares on the train. The manager decided to collect data on arrivals and service times over a number of days, and her figures are summarized

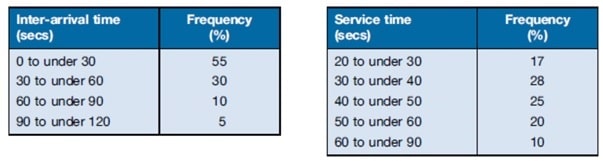
Required

1. Compute the midpoints for arrival and service times and construct the appropriate random number mappings for the random variables starting from 00. (3 marks)
2. Simulate 15 customers arriving at the using the random numbers given below. (12 marks)
3. What is the average time a customer waits for service? (1 mark)
4. What is the average time a customer is in the system (wait plus service time) (2 marks)
5. What is the percent of time the clerk is busy with customers? (2 marks)

Hint (midpoint for 60 to under 90= (60+90)/2=75 sec)

Use the following headings to complete the simulation

Question 3B

CWD Electronics Inc. sells Ipads , which it orders from Japan. Because of shipping and handling costs, each order must be for 10 Ipads. Because of the time it takes to receive an order, the company places an order every time the present stock drops to 10 Ipad players. It costs $10 to place an order. It costs the company $50 in lost sales when a customer asks for a Ipad and the warehouse is out of stock. It costs $10 to keep each Ipad stored in the warehouse. If a customer cannot purchase a Ipad player when it is requested, the customer will not wait until one comes in but will go to a competitor. The following probability distribution for demand for Ipads has been determined:

The time required to receive an order once it is placed (lead time) has the following probability distribution:

The company has 14 Ipads in stock. Orders are always received at the beginning of the week.

Note ( A lead time of 2 weeks imply that an order placed in week one will arrive in week 4.)

Required

1. Construct the appropriate random number mappings for the random variables starting with .00. (2.5 marks for demand and 1.5 mark for lead time)
2. Simulate CWD's ordering and sales policy for 20 weeks. (12 marks)
3. Compute the average cost of the policy( 4 marks)

Use the following headings

Question 4

CWD Department Store in Kingstown maintains a successful catalog sales department in which a clerk takes orders by telephone. If the clerk is occupied on one line, incoming phone calls to the catalog department are answered automatically by an answering machine and asked to wait. As soon as the clerk is free, the party that has waited the longest is transferred and answered first. Calls come in at a rate of about 10 per hour. The clerk is capable of taking an order in an average of 4 minutes. Calls tend to follow a Poisson distribution, and service times tend to be exponential. The clerk is paid $10 per hour, but because of lost goodwill and sales, CWD loses about $25 per hour of customer time spent waiting for the clerk to take an order.

Part A

Answer the following questions:

1. What is the probability that no customers are in the system (Po)? 2 marks
2. What is the average number of customers waiting for service ( Lq)? 3 marks
3. What is the average number of customers in the system (L)?-2 marks
4. What is the average time a customer waits for service(Wq)? 3 marks
5. What is the average time in the system (W) ?-3 marks
6. What is the probability that a customer will have to wait for service (Pw)?-2 marks g What is the probability that there is exactly 2 customers in the system- 2 marks
7. h) What is the probability that there are more than 3 customers in the system-3 mark

Part B

CWD is considering adding a second clerk to take calls. The store would pay that person the same $10 per hour.

Using appropriate formula for the multiple channel model, answer the following questions:

1. What is the probability that no customers are in the system (Po)? 3 marks
2. What is the average number of customers waiting for service (Lq)? 2 marks
3. What is the average number of customers in the system (L)? 3 marks
4. What is the average time a customer waits for service (Wq)? 2 marks
5. What is the average time in the system (W)? 2 marks
6. What is the probability that a customer will have to wait for service (Pw)? 2 marks
7. What is the probability that there is exactly 2 customers in the system 2 marks
8. Should it hire another clerk? Explain by showing the cost savings - 4 marks