ME 655 Special Problem Set
All the problems in this set are represented with the following diagram, without considering the measurement noise (that is N(s) = 0).
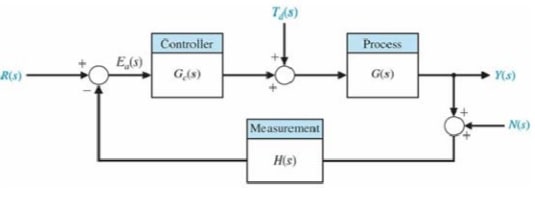
1. Consider the problem of controlling the position of a system with loop transfer function G(s) = 1/s(s+5) with a proportional controller Gc(s) = K. The transfer function of the sensor is H(s) = 1/s/2+1
- Select the gain K to meet the following design requirements based on its response to a step input: (a) overshoot is less than 25% and (b) settling time (with a 2% criterion) is less than 5 seconds. In case the two specifications cannot be met simultaneously, you could compromise by relaxing them by the same percentage, and then select the gain K ( 0) K accordingly.
- Once the value of gain K is determined, check the resulted steady state error due to a step input, or a step disturbance.
- Suggest an approach to reduce or eliminate the steady state error caused by a step disturbance by using a step input.
2. Consider the problem of controlling an unstable system, whose transfer function is obtained as G(s) = 0.1/s2+2s-8. A controller in the form of Gc(s) = K s+6/s+10 with a unity feedback H(s) =1 has been selected for the problem. One of the design objectives is to maintain the output y(t) ≈ 0 when r(t) = 0 in the presence of disturbance. The design specifications, based on a step disturbance, are as follows:
- steady-state tracking error less than 1% in the presence of the disturbance
- settling time (with a 2% criterion) less than 4 seconds, and
- percent overshoot less than 30%.
Select the value of K (K > 0) to meet all the specifications and describe your approach used in your selection process. Plot the results based on your final selection of K value.


