ECO433 Assignment 3

1. Optimal marital sorting on traits: 40 points Suppose that happiness H of a marital partnership between f and m depends only on the wealth W of the two partners. Consider the following two martial output functions:
   
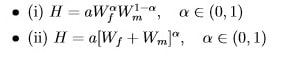
   1. (20) Show whether, in (i) and (ii) respectively, the wealth of the man and the wealth of the woman are substitutes or complements in marital production (or “happiness”).
   2. (10) For a model in which wealth is the only trait that determines marital happiness, which functional form makes more sense to you and why?
   3. (10) Suggest a trait or pair of traits (e.g. W_m could be wealth in stocks and W_f could be wealth in bonds) that would make the other functional form (the one you didn’t choose in (b)) a more realistic representation of the the marital output function of those traits.
2. Quantity and quality and the demand for children: 40 points
   • (20 points) Explain, from a technical point of view, why quantity and quality of children cannot be too close (or “perfect”) substitutes in order for the quantity/quality theory of demand for children to work.
   • (20 points) Explain, from an intuitive point of view, why quantity and quality of children are not likely to be very close substitutes (put another way: are likely to be fairly complementary) in the production of parental happiness.
3. Parental investments in children: 20 points

Using the notes from chapter 6, use equations (1) and (2) on slide 3 to derive “family income” S and the parents’ budget constraint at time t in terms of Z and I_t+1 (equation (*)). Interpret (∗) and explain how it differs from equation (1).