ECMT1020 Written Assignment

Assignment Question

You have been employed as a summer intern by Greater Union cinemas. Your new boss hears you have taken Economics and Business Statistics B and wants you to do some analyst work on sales information they collected back in 2007 but never did anything with. The file ‘Cinema data.xls’ contains two months data for all films which played at George Street cinemas between January 1, 2007 and 28 February, 2007. The data provide daily number of admissions for each film as well as an assortment of other variables including (average) ticket price on each day of observation. The following table provides descriptions of the data provided in the ‘Cinema data.xls’ file:

1. Your first task is to estimate the own-price elasticity of demand. You go back through your old microeconomics notes and find the following equation for elasticity of demand:

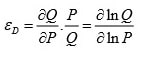
   You take a trip to university to ask your econometrics professor what this equation means as it’s been a while since you took microeconomics. He tells you that if you run a regression with the (natural) logarithm of admissions as your dependent variable and the (natural) logarithm of price as your independent variable, the estimated coefficient will provide you an estimate of the elasticity of demand. Do this and present your results. What is the elasticity of demand that you have estimated? What is the 95% confidence interval for the elasticity? Provide an intuitive interpretation of this confidence interval.

2. You take the finding to your new boss. Your boss also took econometrics at university also, and on seeing your R² suggests you try adding some more variables to the model. He suggests the film’s budget, week-of-release, whether or not the film is a sequel, critical review score, and star (appeal) are all variables which might influence the attendance of a film and could be included in your model. Add these variables into the regression model you estimated in part a). [Note: You should transform budget into natural logarithm before you do the regression.] What is the new value of R²? Test at 1% level of significance whether each of the added variables have coefficients which are statistically different from zero. What do your estimates suggest about the relationship between attendance and each of these additional variables?
3. That evening you call your friend to see what their plans are for the weekend. They tell you they might be going to see a film, but add they hate going to the cinema on the weekends because it is always crowded. That gives you an idea, to create and add three dummy variables to control for increased attendance on Friday, Saturday and Sunday (treat all other days as the reference category). Are these new variables individually significant in the new model? Do the coefficients’ signs support your intuition of increased attendance on the weekends? Which day appears to have the greatest affect on admissions?
4. The next day you show your results to your new boss. He is impressed with your thoughtfulness and likes the additional variables in the model. He pauses and thinks for a minute, “You know what we also see in this business,” he says, “more people going to the movies on opening days, and also we see higher attendance on public holidays and in school holiday periods. Can you include controls for these three things as well?” he asks. Add these three dummy variables into your model from part c) and report on the individual significance. Do the results confirm your boss’s intuition?
5. The weekend has finally come and you have a trip to the beach planned. However, it is rainy and cold. You ring your friend who suggests a trip to the movies instead. You go to see the latest Kick-Ass movie but apparently so did the rest of Sydney. Your friend comments, “It’s always more crowded at the movie when the weather is crappy”. You have a light-bulb moment and decide to include two controls for weather in your model: 1) the difference between the daily maximum and the monthly average maximum (maxtoavdiff); and 2) the daily recorded rainfall (rainfall). Perform a partial-F test to see whether these two additional variables should be included in the model at the 5% level of significance.
6. You decide to present the model you estimated in e) to your boss. He loves it and wants to use it to forecast the following Saturday’s admissions for a film currently screening. For that day only they will offer a discounted ticket price of $12 for all patrons. He also provides you with the following information
   1. The film has a budget of $200,000,000.
   2. The film is in week thee of release.
   3. The film features an A list actor.
   4. The film got a critical review score of 4 (i.e. 4/5).
   5. The film is a sequel.
   6. The weather will be average temperature with zero rainfall.
   7. The film is not an opening day release.
   8. The Saturday does not coincide with a public or school holiday.

   Calculate a point prediction of how many people will attend this film given all of the information above.

   (Hint: be mindful of the (natural) log transformations you have made for admissions).^[1]

7. Before you present the results to your boss, you remember from your ECMT1010 course that it would be better to provide an estimate of the average value of admissions (for the given values of the independent variables) by presenting a confidence interval for the conditional mean (recall equation 13.12 in Black 2E/3E). Because you’ve been paying close attention in class, you realise the confidence intervals computed by KaddStat are not the ones you are after and the equation you learnt in ECMT1010 is only suitable for simple regression, and not multiple regression.

You pay another visit to your econometrics professor who is rushing out the door on the way to the faculty Christmas party. He knows you’ve been learning some matrix algebra so scribbles down an equation in matrix form for the confidence interval for the conditional mean:

[1] You can use the exponentated log prediction as the actual point prediction you are asked to find. That is, you can assume E(y_i|x_i)=exp{`E(log(y<sub>i</sub>|x<sub>i</sub>))`}. [More detail: In statistics there is an issue with the taking the expectation of a log (non-linear) transformation to recover the underlying prediction of interest. In particular, E[log(Y|X)] does not equal log E(Y|X). This is known as Jensens’ inequality. Depending upon assumptions a correction factor may be used, but without this there is no consensus on the 'best' way to handle this problem].