CSCI 360 Frequency and Text Classification using the Substitution Cipher

1 The Main Idea

It is important to be able to tell whether a given document is encrypted or not. This may seem ridiculously obvious, but there are actually some challenging issues involved.

Consider the situation in which a cryptanalyst is doing a key search trying to find the decryption key for a given bit of ciphertext. For instance, maybe we know that ACIE IXL WIXO I WRTBXL is ciphertext resulting from running the substitution cipher with an unknown key on an unknown plaintext.

Suppose, for the sake of argument, that we could think of nothing better for decrypting this ciphertext than to try all 26! keys. How would we know when one of them worked? If we knew that the plaintext was an English word then we could check for English words, or a letter frequency distribution similar to that of English. Thus we could automatically detect genuine decryptions, or at least detect the most likely keys.

We ran into this very situation with the shift cipher, where the keyspace had 26 possible keys for the ciphertext. This number of keys is small enough to admit an exhaustive “brute force” key search, but we’re left with the problem of telling “automatically” whether or not a given key has worked.^[1]

This is one of many places where statistics plays a role in cryptography. It may be that we know that the plaintext belongs to a certain family of documents (e.g. documents written in English), and it is possible to use the statistical profile of the family to identify successful decrypts.

This project is about writing code to tell if a document belongs to a given family of texts by using statistics, and using this profile to implement a hack of the substitution cipher.

2 Instructions

At the end of this project I will expect you to turn in a .zip file containing the following:

• A txt file containing the first and last names of every member of your group, as well as your group number.
• All of your code. You will be graded on whether or not it executes with the correct outputs.
• A short report on your findings. It does not need to be long, it just needs to contain all of the information specified in bold below.
• The decrypted version of the encrypted file you are given.

Your file should be submitted to me with the title project1_lastname with all of your group members last names.

3 Statistical Profiles

We need to be able to do at least two distinct things:

1. Produce a statistical profile of a given document.
2. Compare that profile against other profiles for the purposes of classification.

A statistical profile can mean many things. We have already seen a statistical profile of a document which consisted of the single letter frequency distributions. But what about the distribution that results from taking the characters two at a time (bigrams)? Or three at a time (trigrams)? These are different statistical profiles that capture more information about a document (at the cost of needing a longer document to get accurate values). There are a virtual infinity of statistical analyses that might be done to characterize a document, and these are just three examples, but they are already quite powerful.

Once you have a statistical profile of some kind, what do you do with it? In our case we would want to see if it matches the profile corresponding to the family of plaintext documents. What the plaintext documents are like will depend on the particular application. They might be letters written in English, electronic bank transactions, http protocol exchanges, etc. For the sake of simplicity, let’s say we want to be able to tell whether a given document is English prose. One way to do this is to this is the following:

1. Build a statistical profile P of English prose offline by using a large sample, maybe from Project Gutenberg or some other source.
2. Build a statistical profile P ⁰ of a purported message decrypt M which may or may not be the actual plaintext. Maybe M comes from trying out some candidate key which may or may not be the right key.
3. Somehow measure the “distance” d = d(P,P ⁰) between P and P ⁰.
4. If d is small then we say that M is English, and a true decrypt. If d is large, then we discard P ⁰ and try decrypting with another key.

The only step in this process that may be mysterious is the 3rd one – measuring the distance between two statistical profiles. This is a little technical, but not super technical. We need a little bit more precision in our discussion.

By “statistical profile” we actually mean something more precise, namely a probability distribution. As discussed in class, a probability distribution is just a set of possible outcomes Ω = {`x<sub>1</sub>,x<sub>2</sub>,...,x<sub>n</sub>`} together with probabilities P(X = x₁),P(X = x₂),...,P(X = n), which represent the likelihoods of the respective outcomes occurring. The symbol X represents the (as yet unknown) actual outcome. Thus the fancy looking P(X = x₁) is just saying “the probability that the outcome is x₁”, and similarly for x₂,...,x_n.

This is a little confusing because it is so general. Here are some examples:

{`
3.1 Coin Flip with Fair Coin
Ω = {H,T}
P(X = H) = P(X = T) = 1/2
3.2 Role of One Fair Six Sided Die
Ω = {1,2,3,4,5,6}
P(X = 1) = P(X = 2) = P(X = 3) = P(X = 4) = P(X = 5) = P(X = 6) = 1/6
3.3 Role of Two Fair Six Sided Dice
Ω = {2,3,4,5,6,7,8,9,10,11,12}
`}

Below is the probability P that the roll of two fair six sided dice will add up to Ω.

3.4 Other Representations

Notice that in all of these cases, what the distribution comes down to is just a list of real numbers in the interval [0,1] that sum to 1. For example, in Fair Coin Flips the list is

Note that in each case, the entries sum to 1, which is what makes these probability distributions instead of just number lists.

With this way of representing a probability distrubution it is implicit that Ω = {`0,...,n − 1`} where n is the length of D, and P(X = i) = D[i]. This loses no generality, since the numbers in Ω can mean whatever you want. Maybe 0 means “tails”, 1 means “heads”, etc. It doesn’t really matter except to a human being. Using other kinds of Ω, such as Ω = {H,T}, is really just a psychological convenience – the “math” doesn’t care what you call the possible outcomes, only that they are different symbols. The symbol set Ω = {`0,...,n − 1`} will work as well as any other symbol set of size n.

3.5 A Notion of Distance

Suppose someone gives us a rusty old coin and we want to know whether or not it is a “fair” coin.

That is, does the probability of heads equal 1/2 or not? We do some number of experiments (say 100 coin flips) and we find that heads comes up 59/100 times. Is this good evidence that the coin is not fair?

If this was a statistics class I would explain about the p-test and statistical hypothesis testing, which many people hopefully have seen before.^[2] But in this lab we will use a “lazier” approach.

We will compute the Bhattacharyya distance between our observed probability distribution D_o = [59/100, 41/100] and the distribution of the fair coin, namely D_f = [1/2, 1/2]. Based on the definition of Bhattacharyya distance (given below) this is computed as

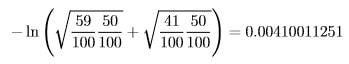
What does this output mean? Figure 1 provides some context by showing how Bhattacharyya distance changes as the number of observed heads out of the sample of 100 increases.

You can see from the figure that when the number of heads is close to 50, the empirical distribution is “close” to [1/2, 1/2] with respect to Bhattacharyya distance, and when the number of heads is far from 50, the distribution is “far” from [1/2, 1/2] with respect to Bhattacharyya distance. Of course this still leaves the question of how close is “close enough”.

We need to come up with some threshold for how far (in terms of Bhattacharyya distance) an empirical distribution can be from [1/2, 1/2] to still be considered as plausibly drawn from the same distribution. This is something we have to determine empirically using some test data, on a case by case basis.^[3]

In general, Bhattacharyya distance between two probability distributions D₁ = [p₁,p₂,...,p_n] and D₂ = [q₁,q₂,...,q_n] is defined by

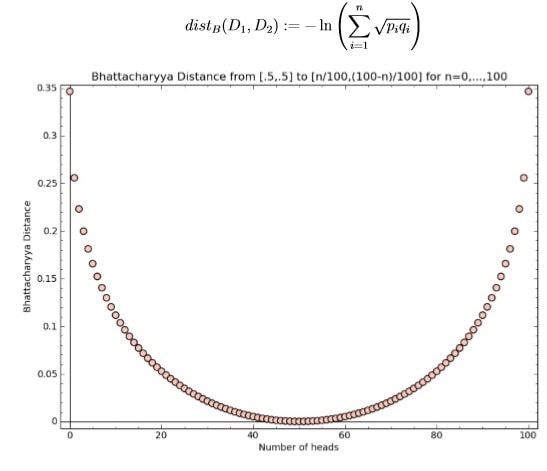
Figure 1

It may help your understanding to confirm that when D₁ = D₂ the distance is zero, which is to be expected. You should be easily able to code this up when D₁ and D₂ are arrays of floats. In fact why don’t you do that right now?

3.6 Challenge 1

Implement a function with C prototype float bhatt_dist(float D1[],float D2[],int n) or with Python prototype def bhatt_dist(D1, D2, n) which computes the Bhattacharyya distance between D1 and D2, as described above. You should be able to use D₁ = [1/2, 1/2] and D₂ = [59/100, 41/100]as a test case (the correct output is given above). You will need to include the math library, which is done like this in C:

#include <math.h> and in python: import math

The main function you will need from math.h (C) or math (Python) is the natural logarithm, which is denoted log in math.h (C), or as math.log (Python). To compile a program which uses the math library you must append -lm to your compilation command, as in gcc file.c -lm for C implementations.

3.7

In order to use our new function for the substitution cipher, we need some probability distributions. For us these will just be float arrays of length 26. That is, float D1[26]; // I will be a probability distrubution

in C, or an array called D1 in Python which contains 26 entries.

The understanding here is that D1[c] for the letter c will be the relative frequency of c in some given document.

3.8 Challenge 2

Write a function that takes a filename and creates a single letter frequency distribution for all the chars (i.e. bytes) occurring in the file. Such a function in C might look roughly like the following:

{`
void mkdist(float* D,char* filename)
{
FILE *fp = fopen(filename,"r");
/*write some code here to initialize some things*/ while((c=fgetc(fp))!=EOF) {
/*write some code here to process the char c*/
}
/*write some more code here to finish things up*/ fclose(fp);
}
`}

I give you this code mainly to stop you from worrying about how to open a file, read from a file, and close the file. All of this is done for you – but you still need to write the actual code to build the probability distribution. Remember that at the end of the method D[i] should be the number of occurrences of i in the file, divided by the total number of bytes (chars) in the file.

Note that we wrote a Python implementation last class which opens a document and saves this distribution in a file. If you are using Python, you may modify this code to return a list of 26 numbers corresponding to the count of each letter in the alphabet.

3.9 Challenge 3: Statistical Analysis of Files

Write a program that takes two filenames as inputs. The output of the program should be the Bhattacharyya distance between the single letter frequency distributions resulting from each of the files, respectively.

Note that to implement this, you will need to use the two functions defined in the first two challenges.

3.10

You have three files in your folder: sample.txt, enc1.txt, and enc2.txt. The file sample.txt is a large sample of writing in English which you will use to build a statistical profile for letter distribution in the English language. Of the other two files, one is an encryption of a document written in English and one is a random collection of letters.

To see what all this is good for, run the Bhattarchaya distance function on the three text files provided to your group. Find the distance between sample.txt and enc1.txt, and the distance between sample.txt and enc2.txt. In your written report, write down the results of these two comparisons and analyze what these results mean. Exactly one of these files is an encryption of a document written in English. In your report, explain which file is the file written in English and justify your reasoning.

3.11 Challenge 4: Decrypting the File

Your next project is to decrypt the file which you determined is in English. You do not know the key. However, you have run a statistical analysis of the file. There are multiple methods to deduce the key:

• Compare the distribution of the encrypted letters to the distribution of English letters that you deduced from txt. For instance, if E is the most common letter in the English language then it would make sense to assume that the most common letter in the ciphertext is the value for E.
• Look at the ciphertext and observe patterns in the words. Single-letter words are likely to be encryptions of the one-letter English words A or I, while a frequently seen three-letter word ending in the encryption of E deduced above is likely to be THE. Get as creative as you wish!

Test different keys which you determined using the above methods until you find a decryption of the text. You will see that the text is a classic work of literature. Write the name of the book you decrypted in your report, the key you deduced, and explain the process you used to find the key.

[1] Try to ignore the fact that with this toy cipher there are other ways to get around this problem – with more serious ciphers there may not be.

[2] If you haven’t, an hour spent reading the Wikipedia article on the p-test would be time well-spent.

[3] The well known p-value takes a user defined threshold as input as well, when used for statistical hypothesis testing.