CS 261/MATH 261 Methods of Numerical Analysis

Assignment 3

(8 marks) Let the functions g₁ and g₂ be defined by

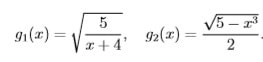
• Show that 1 is a fixed point of g₁ and g₂, and that any fixed point of g₁ or g₂ is a root of the equation x³ + 4x² − 5 = 0.
• Suppose that we take x₀ sufficiently close to 1 (but not equal to 1) and would like to generate a sequence {x_n} by the fixed-point iteration x_n = g₁(x_n−1) (n ≥ 1) or by the fixed-point iteration x_n = g₂(x_n−1) (ⁿ ≥ 1). If you wish to have faster convergence (to the point 1), which of the two fixed-point iterations would you choose? Justify your answer. (You need to make your choice by a theoretical result, not by comparing the first few iterates.)

2. (6 marks) Let g(x) = (2x² + 3)^1/4.
   • Let p₀ = 1. Find p₁₀ by the fixed-point iteration

p_n+1 = g(p_n) (n ≥ 0).

(You should use MATLAB to do this. But just report p₁₀ with at least 10 digits. )

• Let = 1. Use Steffensen’s method to find and. (You should use MATLAB to do this. But just report and, with at least 10 digits. )
• Show that √3 is a fixed point of g. Which of p₁₀ and gives a better approximation to this fixed point?

3. (6 marks) Let f(x) = x⁴ + 3x³ − 4x² + 3x − 2.

Find f(1.6) and f^′(1.6) by Horner’s method using a table form (with the help of a calculator).

4. (5 marks) Let f(x) = x³ −x−1 and x₀ = 1.1,x₁ = 1.2,x₂ = 1.3 be approximations to a solution of f(x) = 0. Use Mu¨ller’s method to find the next approximation x₃.
5. (5 marks) Suppose that Newton’s method is applied to find the solution p = 0 of the equation = 0. It is known that, starting with any p₀ > 0, the sequence {p_n} produced by the Newton’s method is monotonically decreasing (i.e., p₀ > p₁ > p₂ > ··) and converges to 0.

Prove that {p_n} converges to 0 linearly with rate 2/3. (hint: You need to have the patience to use L’Hospital rule repeatedly. )