Quadratic Equation Assignment Help

Quadratic Equation Introduction

A quadratic equation is a second-order polynomial equation in a single variable x

ax² + bx + c = 0,

With a ≠. Because it is a second-order polynomial equation, the fundamental theorem of algebra guarantees that it has two solutions. These solutions may be both real, or both complex.

Quadratic formula and its derivation:

The roots ‘x’ can be found by completing the square,

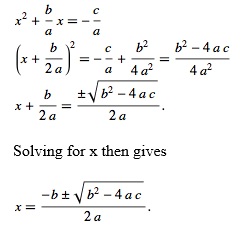
This equation is known as the quadratic formula.

An alternate form of the quadratic equation is given by dividing (◇) through by x2:

a + b/x + c/x² = 0

c(1/x² + b/cx) + a = 0

c(1/x + b/2c)² = c(b/2c)² - a = b²/4c - 4ac/4c = b² - 4ac/4c

Therefore,

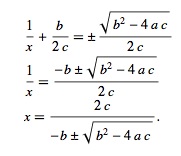
Now consider the equation expressed in the form

a2 x² + a1 x + a0 = 0,

With solutions and. These solutions satisfy Vieta's formulas

z1 + z2 = - a1/a2

z1z2 = a0/a2

Coefficients of Quadratic equation:

A quadratic equation with real coefficients can have either one or two distinct real roots, or two distinct complex roots. In this case the discriminant determines the number and nature of the roots. There are three cases:

If the discriminant is positive, then there are two distinct roots

-b + √∆/2a and -b - √∆/2a,

If the discriminant is zero, then there is exactly one real root

-b/2a, Sometimes called a repeated or double root.

If the discriminant is negative, then there are two distinct (non-real) complex roots and no real roots.

-b/2a + i√-∆/2a and -b/2a - i√-∆/2a,

The properties of the symmetric polynomials appearing in Vieta's formulas then give

z²1 + z²2 = a²1 - 2a₀ a2/a²2

z³1 + z³2 = - a³1 - 3a₀a1a2/a³2

z⁴1 + z⁴2 = a⁴1 - 4a₀ a²1 a2 + 2a²₀ a²₂ / a⁴₂