PSTAT 171 Theory of Interest
Interest Theory deals with the time value of money.
Under normal
circumstances (which have been lacking since 2008) capital is scarce.
Like every other commodity it has a price. The price
that we pay for the use of capital is called
“interest,” that is the price you have to pay the user
of capital to lend it to you. Of course, because you will have to pay
back the capital in the future you will want to put it to good use, and
to earn a return on capital or yield
(which should be higher than the price you pay for borrowing, or its not
worth
borrowing).
Interest may also be thought of as the rate that balances consumption
between periods. For example, you have all made the decision to attend
university, a decision that has a cost to it (not just the residence and
tuition that you pay, but the income that you forego). You expect to
receive a greater reward in the future to make up for the deferral of
your enjoyment today. We can actually analyze this decision when we have
developed a few tools (it’s a bit complicated now). Here is a simpler
example: You could buy a Starbucks latte for $3.00 today; what would I
have to pay you to defer your enjoyment of the Starbucks latte to
tomorrow? You are unlikely to be willing to do it for $3.00. But maybe
if I paid you $4.00 you would consider it. If so, the implied interest
rate is 33% daily (rather a high rate, but its an example).
So we have seen that interest is a price; both the price that you
would have to pay to borrow money, and the price that you demand in
order to defer your
consumption into the future. Because we are looking at decisions made
over time this price is also known as the time value of money.
There are two types of interest:
a. Simple Interest. If you deposit 100 in a bank at 6% interest, your capital will earn $6.00 at year-end, and you will have $106. If you choose to leave your money on deposit, another $6.00 will accrue by year-end 2, so now you will have $112.00 (assuming you haven’t withdrawn anything).
b. Compound Interest is more common. By leaving your $6.00 on deposit at year-end 1, you will accrue “interest on the interest” by year-end 2. In addition to the $6.00 that you earn in year 2 from your capital (also called
principal), you will earn 0.06 * $6.00 or $0.36. So in the compound case you will have $1.1236, vs. $1.12 in the simple interest case.
TIP: Something you will find useful in this course, and in actuarial work in general (which deals with values at different time periods) is the time-line. In the simple examples above, we could draw a time-line and visualize how interest is accruing:
Simple
| $100 | $106.00 | $112.00 |
|---|
|_______________________________|________________________________|
| 0 | 1 | 2 |
|---|
Compound
| $100 | $106.00 | $112.36 |
|---|
|_______________________________|________________________________|
| 0 | 1 | 2 |
|---|
Of course, in the one-year case with simple interest there is no difference between the amount on deposit at the end of the year: the effective rate in both cases is 6%. The difference only arises in year 2, or (as we shall see later) if the interest is compounded during the year.
In terms of formulae, simple interest accumulates to:
100[1 + (0.06)n] at the end of n years while the same amount at 6% compounded annually accumulates to:
100 (1.06n) after n years.
Similarly, we can reverse the equation and ask: how much would I have to invest now to have $100 at some point in the future. In the one-year case, the answer is easy, and applies whether we are earning simple or compound interest. Let the amount be P (principal). We know that 100 amounts to 100(1.06) at the end of
1 year whether interest is simple or compound. So P amounts to P(1.06) and we
| want to have 100 at the end of 1 year, P has to equal 100/1.06, or | 100( 1.06. 1 ) |
|---|
In this case, P = 94.34. You can check the math by multiplying 94.34x1.06 = 100.
| Actuaries have a name for the term | | 1 | by the way. We call it v . We will use | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| | 1.06 | | |||||||||||||||||
v throughout this course to represent the present value of an amount of 1 due one year hence.
What if we want to have 100 in 2 years’ time? Again, let the principal amount be P.
If at simple interest, we know that the interest accrues at P(0.06) annually and after 2 years I have interest of P (0.06)(2) or 0.12P. In total, I have 1.12P and this
| equals 100, so 100 | = | P | (1.12) => | P | = | 100 /1.12 or 89.29. |
|---|
You can check this: interest in year 1 = (0.06)(89.29) or $5.36. After 2 years interest is $10.72, which (together with the principal of $89.29) gives us $100.01.
Tip #2: always check your answer for reasonableness (is it in the right ball-park?) and accuracy using a different method (i.e. not simply repeating the same calculation).
Tip #3: its difficult to recommend a simple rule regarding decimal places. When you are dealing with dollars, 2 is probably enough in most cases. I prefer fewer rather than more.
What if we earn compound interest? Well, now we know that after 2 years the original principal will have accumulated to P(1.06)2and is equal to 100, so
| P | = | 100 /1.06 | 2 | or | $89.00 | . We can check this independently, as above by doing an |
|---|
interest calculation, but more important, we know that the total interest earned when compounded is greater than simple interest, so the principal required to be
4
invested should be smaller, which it is: $89.00 vs. $89.29. The two numbers, however, should be close because as we saw previously, the difference between simple and compound interest on $100 for 2 years at 6% is only $0.36.
If we had been paying attention to the first year example, we could also have written this expression in actuarial terms as:
| P = | 100/1.06 | 2 or 100 v | 2 | . We would have derived the same answer because | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| v | 2 | = | | 0.889996 | = $89.00. | ||||||||||
| 1 | | = | | 1 | | = | |||||||||
| | 1.06 | 2 | | | 1.1236 | | |||||||||
Some actuarial notation
Actuarial notation is different and important, as you will see in this course and in 172, if you progress. It is useful because it allows actuaries to communicate precisely and at the same time in “shorthand.” Consult the SOA reference in the introductory material for the notation required for the SOA exam FM.
| By the way, you will sometimes see v written as | v 0.06 | , just to be extra precise |
|---|
about the value we are talking about (especially when more than one interest rate is involved). There is also no shorthand term for 1 i+ . We just write 1 i+ !
If you go on to become an actuary you will use this throughout your career –hardly a day goes by when I don’t do a calculation with 1 i+ or v !
Example 1
a. What is the present value of $20,000 payable in 15 years at 5% per annum compound?
b. What will $5,000 amount to in 6 years at 5% annually compound? Write this problem in actuarial notation.
c. How much will I have to invest to accumulate to $5,000 in 10 years time at 5% compound interest? Write this problem in actuarial notation.
5
Answer:
a. 9,620.34
b. 6,700.48. 5000(1+i)6 0.05
c. 5000 v10 0.05= 3,069.57
Define:
a t the amount to which an initial investment of 1 grows by time t ≥ 0; and
| A t the amount to which an initial investment of | A (0) | grows by time t. |
|---|
Then for compound interest:
| a t ( ) | = | (1 | + | i | )t | and | A t ( ) = (0)(1 | + | i | )t |
|---|
And for simple interest:
| a t ( ) = (1 | + | it | ) | and | A t ( ) = (0)(1 | + | it | ) |
|---|
Effective Rate of Interest
We can find the effective rate of interest over any time period. For the period
[t,t+1] the beginning amount is A t and the amount at the end of the period is
A t +1) . Interest earned over the period is A t+1) - ( ) . The effective rate of
interest over this period is
| i t | +1 | = | amount earned | = | A t | + | 1) | − | A t ( ) | = | a t | + | 1) | − | a t ( ) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| beginning amount | A t ( ) | a t ( ) | |||||||||||||
Example 2
We assume that we earn 6% over the time interval [1,2]. Principal = 1.
Note that this is year 2, so we begin the period with accumulated principal of 1.06.
What is the effective rate of interest over the two years, assuming a. compound interest at 6% and b. simple interest at 6%?
Solution
| a. Compound: | i | = | a | (2) | − | a | (1) | = | 0.0636 | = 0.06 | |||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | a | (1) | 1.06 | ||||||||||||||||||||||||||||||||||||||||||||||
No surprise here: if the effective rate is 6% compounded annually, then measuring the effective annual rate earned over two years has to be 6%!
| b. Simple: | i | = | a | (2) | − | a | (1) | = | 0.06 | = 0.0566 | |||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | a | (1) | 1.06 | ||||||||||||||||||||||||||||||||||||||||||||||
Notice that the effective rate of interest in the case of compounded interest is the rate itself; in the simple interest case it is the equivalent compounded rate.
Example 3
a. A savings account offers simple interest of 10%. How long does it take to double your principal?
b. Repeat the same calculation but assume compound interest.
Solution
a. Assuming simple interest, after n year the accumulated amount is a(n) = (0)(1+ni ) and ( ) / (0) = 2.0
So (1+n (0.1)) = 2.0 and (0.1)n = 1.0 so n = 10.
Again, no surprise here. In the general case, the number of years (n) | n | = | 1 | . | |||||
|---|---|---|---|---|---|---|---|---|---|
| i | |||||||||
b. Assuming compound interest | a(n) = (0)(1 | + | i | ) and ( ) / (0) = 2.0 | |||||
| (1+0.1) = 2.0 | => n (ln 1.1) = ln 2 => n = ln 2.0/ln 1.1 | ||||||||
And n = 7.2725.
In the general case, (1+ ) = 2.0 => n [ln (1 | + | i | )]= ln(2) | |
|---|---|---|---|---|
| | 0.693 | |||
The power of compound interest: note how much more quickly you double your money with compound interest!
Nominal and Effective Rates of Interest
In cases where payments are made for periods less than a year, or when compounding is performed more frequently than annually (e.g. monthly or quarterly) rates are quoted as nominal annual rates and then converted to a periodic rate.
For example, if you earn 10% annually, compounded quarterly, you will earn 2.5% for the first quarter, then 2.5% multiplied by the 1.025 in the second quarter, and 2.5% multiplied by (1.025)2in the third quarter, etc. The following time-line may help your understanding
Compound
| $1 | $1.025 | $1.05062 | $1.076891 | $1.103813 |
|---|
|_______________|________________|________________|________________|
| 0 | 1/4 | 2/4 | 3/4 | 4/4 |
|---|
In this case, the nominal rate is 10% (0.10). The periodic rate (compounded quarterly) is 0.025 or 2.5%. The annual effective rate is (1+0.10/4)4= 1.103813. Thus the yearly effective rate is 10.3813%.
This is an example of a 10% nominal rate, compounded quarterly. A principal of 1 will accumulate to 1.103813 by the end of the year; so in terms of the definition,
| a t | + | 1) | − | a t ( ) | = | 1.103813 1.00 | = 10.3813% | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a t ( ) | 1.00 | ||||||||||||||||||||||||||||
As we see: the effective rate is higher than the nominal rate when interest is compounded more frequently than annually. Effective rates are calculated as compound rates; so if simple interest is credited, the effective rate will be less than the nominal rate, as the next example shows.
Example 4
Assume you earn a monthly rate of 1% compound. a. What is the annual
nominal rate?
b. What is the annual effective rate?
Solution
a. Annual nominal rate 12%.
b. Annual effective rate = (1.01)12– 1 = 12.6825%.
You will encounter effective rates in bank and credit card advertisements. Here is an example (from Citibank):

In this case 12.99% (or 21.99%) are Annual Percentage Rates (APR) or effective
annual rates. We now know that we can calculate the nominal annual rate that is
equivalent to these APRs:
12.99% is the effective annual rate. For credit cards, the nominal rate is
compounded monthly (accrued interest is calculated each month on your outstanding balance). So 1.1299 = (1+ i(12)/12)12.
New notation: we denote a nominal interest rate compounded m times per year as i(m).
(1+ i(12)/12) = 1.12991/12= 1.010229
i(12)/12 = 0.010229
i(12)= 12.275.
So the annual nominal rate equivalent to the effective APR 12.99% is 12.275%.
Moral of the story: not a good idea to accumulate credit card balances.
In the general case of m payments per year, the nominal rate is i(m)and the periodic rate is i(m)/m. The effective rate is:
| (1 | + | i | ( | m | ) | ) | m | − | 1 | |||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m | ||||||||||||||||||||||||||||||||||||||||||||
| | 1 | + | i | = (1+ | i | ( | m | ) | ) | m | |||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m | |||||||||||||||||||||||||||||||||||||||||||||||||
Example 5
a. Assume i(12)= 6%. What is the effective rate i?
b. If the effective rate i is 5%, what is i(12)?
Answer: a. 6.168% b. 4.889%
Formulae: a. effective rate i = (1.005)12-1
b. = ((1.05)1/12-1 ) *12 => i(12)= 0.0489
Note: it is important to be comfortable with the concept of equivalent rates and
rates compounded more frequently than once per year because most rate are.
This is an important and tricky part of this course - make sure you understand the
examples and the homework.
11
Discount Rates
We saw earlier that we would have to invest an amount < $100 at interest of 6% to accrue $100 at the end of the period. Assuming a one-year period, we would need to invest $94.34, which would attract interest of $5.66 to add to $100.
Terminology: The rate that is applied to $100 to determine the present value at time zero is called the discount rate. The discount factor (we have met before) is v; the discount rate, however, we define below:
Important Definitions (memorize this)
We define the discount, or present value factor as v. v = 1/1+i (as we saw above).
Then the rate of discount or d = 1 - 1/1+i = 1-v = i/(1+i) = i v
(these are all equivalent; just different ways of calculating d; make sure you know them all.)
Discount rates can be confusing – accountants, for example, refer to
the
“discount rate” as the rate (that we now know is the interest rate) when
they are talking about the discounting process, which leads to confusion
between i (the annual interest rate used to calculate the
discount) and d, the discount rate.
In terms of the example above, the present value amount that we need
to hold at 6% to accumulate to $1 is 100 (1/1.06) = 94.34. The interest
rate in this
calculation is 6%; the present value factor (v) = 0.9434 and the
discount rate is d = 1-0.9434 or 0.0566. Multiplying by 100, the amount
of the discount in this case is $5.66, which is the amount we can
discount the $100 by to determine the principal required to accumulate
to $100 by the end of the period. Note the difference between the
interest and discount rates, and the fact that the present value and
discount factors are the same.
Some students are confused by the difference between interest and discount rates. The following real-world example may help to understand the difference:
12
If you were running a store, you would mark up your products at some rate (to cover your costs and profit). Let’s call that rate “i” for now. Assume that the product costs $100; you mark it up at i=25%. So the marked up or retail price is now $125. To find the original cost of the item, however, we do not discount the retail price at 25%. The original price divided by the selling price is 100/125, or 80%. 80% of course is = 100 - 20, hence the discount rate is 20%. So the discount rate equivalent to the mark-up (or interest rate) of 25% is 20%, which also
| happens to be | 20% | = | 25% | = | i | where = 0.25 and 1+ | i | = 1.25 which is our | ||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 125% | 1 | + | i | |||||||||||||||||||||||||||||||||||||||||||||||||||
definition of d!
As with the interest/discount case, the discount rate is lower than the corresponding interest rate (because it applies to a loaded price).
Example 6
If the annual rate of interest is 10%, what is d?
Solution
Present value factor (v) = 1/1.10 = 0.9091
Then d = 1 – 0.9091 = 0.0909.
Nominal and effective rates of discount
This works the same way as the nominal rate of interest, with one important difference. Define d(m)as the nominal rate of discount, compounded m-thly.
Then
1 – d (= v) = | (1 - | d | ( | m | ) | ) | m | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m | |||||||||||||||||||||||||||||
The key difference to remember is that to calculate the effective rate of interest, we add 1 to the nominal periodic rate (i(m)/m). To derive the effective discount rate we subtract the periodic discount rate from 1.
Example 7
Find the effective annual discount rate corresponding to a nominal rate
of 8%, converted quarterly (“converted” is a synonym for
compounded).
Solution
| 1 | − | d | | d | (4) | | 4 | = (1 - | 0.08 | ) | 4 | = 0.984= 0.9224 => d = 0.0776 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| | 4 | | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Example 8
Find the nominal rate convertible semi-annually corresponding to an
effective annual rate of discount of 6%
Solution
d = 0.06 => 1 - d = 0.94.
| 1 – d = | (1 - | d | (2) | ) | 2 | = 0.94 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
2 | ( | d | (2) | ) | = 0.0305 | ||||||||
| (1 - | d | (2) | ) = 0.94 1/2 | = 0.9695 => | |||||||||
2 | 2 | ||||||||||||
d(2)= 0.0609
Example 9
Find: (first write in actuarial notation)
a. The effective rate of discount corresponding to a nominal rate of
7.5%, convertible 3 times per year. (ans. 7.3141%)
14
(1-0.075/3)3= 0.9269 => effective rate = 1- 0.9269 = 0.0731.
b. The nominal discount rate convertible monthly corresponding to an
annual effective rate of 6%. (ans. 6.17%)
(1- d(12)/12)12= 0.94 => (1-d(12)/12) = 0.00514 and 12(d(12)) =
0.06168 Example 10
Find the rate of discount compounded semi-annually that is equivalent to
a nominal rate of interest of 8%, converted monthly.
Solution
Tip #4: this is a typical exam question; you need to
read the question CAREFULLY.
Although we are aiming to find a discount rate, this rate is equivalent to an effective interest rate. It is easy to miss this and do the calculation in terms of discount rates.
First, we need to determine the effective interest rate corresponding
to the nominal 8% rate; (1 + 0.08/12)12= 1.083; from this we know
that
v = 1/1.083 = 0.92336.
Now, we need to find the nominal discount rate that, converted
semi-annually, is equivalent to the 8.3% rate. (1- d(2)/2)2=
0.92336
(1- d(2)/2) = 0.96092
d(2)/2 = 0.03908
d(2)= 0.07816
Continuous Interest
Assume that interest of 6% is credited annually. Then at the end of the
year, the investor will have 1.06. Effective rate is 6%
Assume that interest is compounded semi-annually; then effective rate is
(1.03)2-1= 6.09%
15
Assume that interest is compounded quarterly: effective rate is (1.015)4-1 or 6.136%.
Assume that interest is compounded monthly: effective rate is (1.005)12-1 or 6.168%.
We note that as the frequency of compounding increases, so does the effective rate of interest. We define the limit, as m -> ∞, of i(m)as δ, the force of interest.
| a t ( ) = (1 | + | i | ) t | = | e t | ln(1+ | i | ) |
|---|
We know that when interest is compounded continuously,
| a t ( ) = (1 | + | i | ) t | => | ln ( ( )) = ln (1+ ) |
|---|
Since = ln (1+ ),
| ln ( ( )) = | t | | a t ( ) = (1 0.06) t | = | e t | ln(1 0.06) | = | e t | (0.058269) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| => | ( ) = et | ||||||||||||
| Also, vt= e | − | | t | ||||||||||
| And assuming 6% annual interest, | |||||||||||||
Note the following: accumulation at the end of year 2 is
e2(0.058269)= e0.116538= 1.1236
But (1.06)2, the accumulated value at the end of year 2, is equal to 1.1236.
So when we are evaluating the accumulated (or present) value after a whole number of years, it doesn’t matter whether interest is compounded continuously or annually. It does matter at fractional durations.
Important definitions (memorize these)
| | = (1 | + | i | ) (t) = et | + | = | v | n | e | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (1 | + | i | ) | n | = | e | n | and (1 | + | i | ) | − | n | = | e | − | n | |||||||||
Note the special case of n=1: (1 | i | )n | = | |||||||||||||||||||||||
This implies that at the end of one year you will earn the same amount at an effective continuous rate of as you will at the equivalent simple rate
of i.
δ is the force of interest.
| | (t) = | a t '( ) | in other words, the derivative of the accumulation function |
|---|---|---|---|
| a t ( ) |
(the rate at which the accumulation function is increasing) at time t, divided by
the value of the accumulation function at (t)). We can also think of this as the
proportional rate of change of the accumulation function at time t.
For the constant force of interest model | a | (t) = et | ||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| | (t) = | | e | t | = | | ||||||||||||||||||||||||||||||||||||||
| e | t | |||||||||||||||||||||||||||||||||||||||||||
And as a reminder:
| n lim (1→∞ | + | r | )n | = | e | r | and | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | |||||||||||||||||||||||||||||
| From elementary calculus we know that | d | ln [ ( )] = | a t ' ( ) | ||||||||||||||||||||||||||
| dt | a t ( ) | ||||||||||||||||||||||||||||
| And from our definition, we also know that | | (t) = | a t '( ) | ||||||||||||||||||||||||||
a t ( ) | |||||||||||||||||||||||||||||
| So | d | ln [ ( )] = | a t ' ( ) | = (t) | and in turn: | ||||||||||||||||||||||||
| dt | a t ( ) | ||||||||||||||||||||||||||||
k | | ( ) dt = ln [ ( )] 0 k | |||||||||||||||||||||||||||
ln [ (k)] - ln [1] = ln [ (k)]
| => e | t | = (t) |
|---|
This last expression allows us to solve problems in which δ varies with time (i.e. δ(t)) rather than being a constant.
When we compare the value of two funds at the end of the year, one credited interest at 6% compounded annually and the other credited the equivalent force of interest, δ = 0.058269, the values were the same. This is true at the year-end (because that’s when interest is compounded in the first case). It is not true of interim points. This is a fairly important point to grasp: in between the points at which interest is compounded (when interest is compounded or converted annually or more frequently during the year) interest accrues on a simple basis (or uniformly). To see how this works, think about what would happen if you deposited $100 with a bank at 6% compounded annually and closed your account after a month. You would earn simple interest at 6% for one month, or 0.005. You would withdraw $100.50. Throughout the year, interest accrues uniformly; by year end, the total interest accrued is 12/12 * 0.005 or 6%; hence at the end of year 1, you will have $106.00. This is true because interest is not earned on the accruing interest.
In the case of interest earned at the force of interest δ = 0.058269 interest is credited continuously and earns interest on the interest continuously. By year end, the fund is the same: eδ= 1.06.
If we were to draw a line during the year, say at mid-year, in the first case the fund would have a balance of 100 + 6/12 * 0.005 = 103.00.
At the same point (mid-year) the continuous case would have an accrued value of e(0.5)δ= 102.9563. Note that this is slightly, but significantly, lower than the first case. Why is this? Because interest is credited (continuously) at the equivalent force of interest, both funds are equal at year-end. But in the continuous case, more interest is earned in the second half of the year than the first, so the balance at mid-year must be lower than the uniform case (in the uniform case, the same amount of interest is earned each day).
Some examples to illustrate the point:
Example 11
Given δ(t) = 2/(t+1), find a t ( )
Solution
| Since | e | t | = (t) | , we first need to integrate δ(t): | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
t∫0 | | (u)du = | t∫0 | u | 2 | 1 | du = 2ln ( u | + | 1)| = 2 ln ( 0 t | + | 1) | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| + | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| So | a t ( ) = e | 2ln( | t | +1) | = | ( e | n( | t | +1) 2 ) | = | (t+1) | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
Example 12
Given δ(t) = 6/(2t+1), find a t .
Solution
| Since | e | t | = (t) | , we first need to integrate δ(t): | + | 1) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
t∫0 | | (u)du = | t∫0 | 6 | 1 | du = | (6)(1/ 2) | ln (2 u | + | 1)| = 3 ln (2 0 t | ||||||||||
| 2 u | + | |||||||||||||||||||
| And | e | t | = e | 3ln(2 | t+1) | = (2t+1) | 3 | |||||||||||||
Checking your results for reasonableness
As I mentioned before, it is critical to develop a practice of checking
the plausibility of your results (not the accuracy. Important
relationships to remember w.r.t. plausibility:
d < d(m)< δ < i(m)< i, i > 0 and m >
1.
Compound interest problems for homework
Example 13
How much should you deposit in your College fund now to have $80,000 in
18 years at 6% interest?
Example 14
If you deposit $1,000 now in a fund earning 5.75%, what will it be worth
in 5 years?
Example 15
You deposit $1,000 in a fund earning 5.75%. How long will it take to
double your money?
Example 16
Bernie Madoff invites you to invest $1,000 in his fund now and be
guaranteed at least $1,500 in 4 years. What is the effective rate that
Mr. Madoff is promising you?
Example 17
Repeat Example 15 but assume that interest is convertible quarterly.
Example 18
How much should you deposit in a bank account earning 5% annually to be
able to withdraw $1,000 in 2 years and 2,000 in 4 years?
Example 19
You deposit $5,000 in an account earning 5% compounded semi-annually for
2 years and 7%, compounded quarterly thereafter. What is the account
value after 7 years?
Example 20
What is the equivalent annual rate, compounded annually, in problem
19?
Example 21
You deposit $5,000 in an account that earns 5% compounded annually in
years 1 and 2, and thereafter at a continuous rate δ(t) = 2/(t+1).
What is the value of the account after 5 years?
Example 22
Suppose an initial investment of $100 grows according to the amount
function A t ( ) = 100 (1+0.01 ).
a. Find the effective rate of interest earned during the 5thyear 5i .
b. Find the effective discount rate during the 5thyear d . 5
c. Find the force of interest t
d. Find the average rate of interest earned during the first five years. Example 23
| Let | ni | = | 0.1 for = 1,2,3,4 | be the effective rate of interest earned in year n. Find |
|---|
a(4) and the effective annual rate of interest earned during the first 4 years. Example 24
| An investment fund has a force of interest | =t | 2 t | . Find the amount of money to |
|---|
be invested in the fund at time t = 1 in order to have $10,000 at time t = 3. Example 25
| An investment fund has a force of interest | =t | 2 t | . $100 is invested at time t= 0. |
|---|
Compute the interest earned in the account during year 2.
Example 26
A fund starts with a zero balance at time zero. The fund accumulates
with a varying force of interest
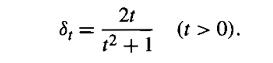
A deposit of $100,000 is made at time 2. Calculate the number of years from the time of deposit for the fund to double.
Example 27
An investor puts 100 into a fund paying an effective rate of discount of
20% for the first 2 years and a force of interest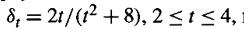 for
the next 2 years. At the end of 4 years the amount in the account is the
same as it would have been if he had put 100 into an account paying
interest at a nominal rate of i
for
the next 2 years. At the end of 4 years the amount in the account is the
same as it would have been if he had put 100 into an account paying
interest at a nominal rate of i
compounded quarterly. Calculate i.
Example 28



