PSTAT 171 Term Structure of Interest Rates Homework
Given the following yield curve, answer the next 2 questions:
Year Spot Rate
1 5.0%
2 4.5%
3 4.0%
4 4.0%
5 4.0%
1. A three year 1000 Par bond with annual interest payments has a coupon rate of 4%. Use the yield curve above to find the price P and the yield to maturity.
Solution
PV = 40/(1.05) + 40/(1.045)2+ 1040/(1.04)3 = 999.28
2. Find the one-year forward rate.
Solution
i 1,2 = s2 2/s1 = 1.0452/1.05 = 1.04
i 1,2 = 0.04.
3. Yield rates to maturity of zero coupon bonds are currently 8.5% for a one- year, 9.5% for two year and 10.5% for a three-year maturity. Calculate the forward rate for year two implied by these current bond yields.
Solution
We want to calculate 1,2 i
= 10.5%
= (1+s2)2/(1+s1)1-1
2
4. A yield curve is defined by the following equation:
ki = 0.09+0.002 k−0.001 k 2 where ikis the effective rate of return for a zero coupon bond of maturity k years.
Find the one-year effective forward rate for year 5 that is implied by this yield curve.
Solution
Note that the question asks in terms of a spot rate of “ik.” We use the terminology skfor the spot rate.
The forward rate (as our notes define) for year 5 is i4,5, which we know is equal to (1+s5)5/(1+s4)4-1.
s4 = 0.082 and s5= 0.075.
Then i4,5 = 1.0755/1.0824-1 = 4.74%
5. You are given the following term structure of spot rates:
Year Spot Rate
1. 5.00%
2. 5.75%
3. 6.25%
4. 6.50%
A three year annuity-immediate will be issued a year from now with annual payments of 5,000. Using the forward rates, calculate the present value of this annuity a year from now.
3
Solution
We can start with a time-line:
|_____________|_____________|______________|________________|
| 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| X | 5,000 | 5,000 | 5,000 |
We want to value the income stream at time X.
We need to calculate a new set of spot rates for the years one-year hence.
(The spot rates that we are given apply today). We will denote them as jn.
Then:
(1+j1) = 1.05752/1.05 = 1.065
(1+j2)2= (1+i1,2)(1+i2,3) = (1.065)(1.0625)3/1.05752= 1.14229
(1+j3)3= (1+i1,2)(1+i2,3) (1+i3,4) = (1.065)(1.14229)(1.065)4/1.06253= 1.2251
PV = 5000 | + | 5000 | + | 5000 | = 13,152.50 |
|---|---|---|---|---|---|
| 1.065 | 1.14229 | 1.2251 |
6. You are given the following n-year forward rates:
Year Forward Rate
1 3.0%
2 4.4%
3 4.8%
4 5.6%
4
a. Find s4.
b. A four-year 1000 par bond is issued with 5% annual coupons. Find the price of the bond using the spot rates calculated in a.
c. What is the yield to maturity of this bond?
Solution
| a. | (1 | + | i 0,1 | )( 1 | + | i 1,2 | ) ( 1 | + | i 2,3 | ) ( 1 | + | i 3,4 | ) | = | (1+s ) 4 | 4 |
|---|
s4= [(1.03)(1.044)(1.048)(1.056)]1/4
4.44%
b. We first need to calculate a series of spot rates:
(1+s4)4= 1.19 => s4 = 4.44%
(1+s3)3= 1.127 => s3 = 4.06%
(1+s2)2= 1.075 => s2 = 3.68%
Then the value of the bond is 50/1.03 + 50/1.075 + 50/1.127 + 1050/1.19
PV = 1,021.77
c. Yield to maturity=> | 50a 4| +1000v 4 | = 1021.77 |
|---|
i= (179.82 + 841.94) at 4.395%
7. The yield to maturity on 5 year annual coupon bonds maturing at 1000 Par is as follows:
Term (years) | Yield |
|---|---|
1 | 6.0% |
2 | 6.5% |
3 | 7.0% |
Calculate the 1, 2 and 3 year spot rates.
5

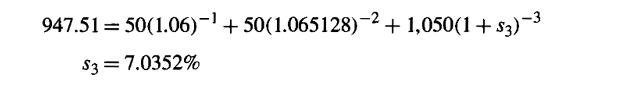
8. | The following are the current prices of $1,000 zero-coupon bonds: |
|---|
Term (years) | Price |
|---|---|
1 | $943.40 |
2 | X |
3 | 805.08 |
If the one-year forward rate for year 2 is 8% (i.e. the one year effective rate during year 2) determine X.
6
Solution

9. The yield rate on a one year zero-coupon bond is currently 7% and the yield rate on a 2-year zero coupon bond is currently 8%. The Treasury plans to issue a two year bond with a 9% annual coupon, maturing at $100 par value. Determine the yield to maturity of the two year coupon bond.
Solution
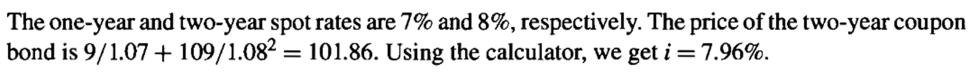
10. | You a given the following information about the Treasury market: |
|---|
Term (years) | Coupon | Yield-to-maturity (nominal annual rate converted semi-annually) | Price |
|---|---|---|---|
0.5 | 0% | 8.1% | $96.11 |
1 | 0% | 8.4% | $92.10 |
1.5 | 9% | 8.6% | $100.55 |
2 | 10% | 9.0% | $101.79 |
Coupons are paid semi-annually. Determine the spot rate for the 1-1/2 year period, expressed as a nominal rate compounded semi-annually.
7
Solution
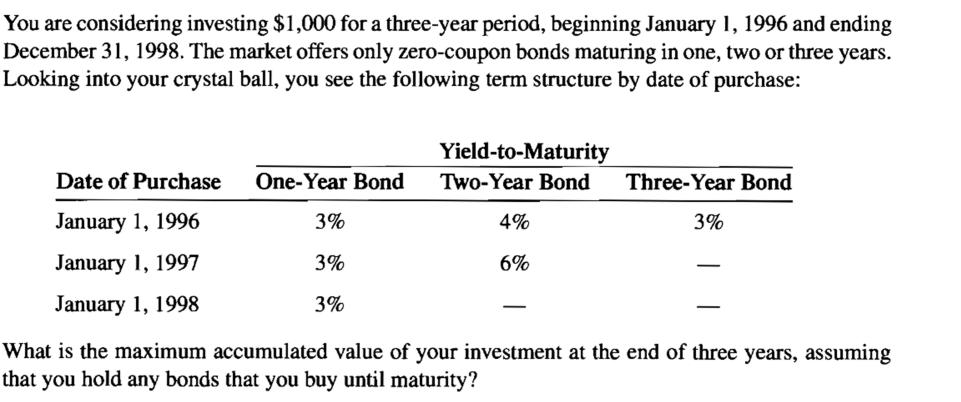
11.

Solution
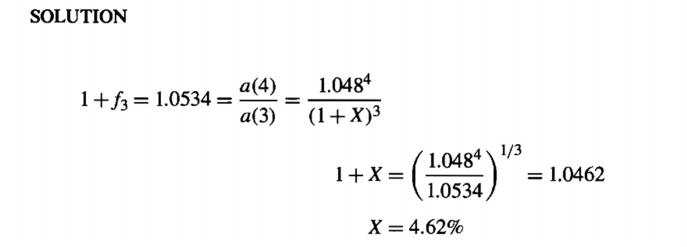
8
12. | You are given the following spot rates: |
|---|
Term (years) | Spot Rate |
|---|---|
1 | 4.00% |
2 | 4.30% |
3 | X |
4 | 4.80% |
If the one-year forward rate for year 4 is 5.34%, calculate X.
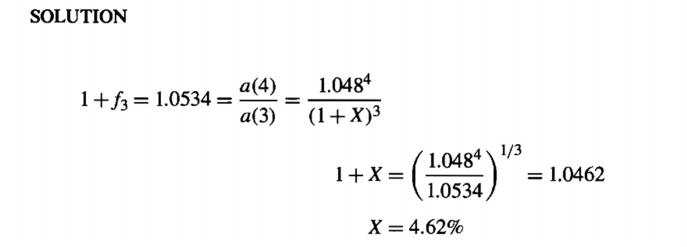
13.

Solution
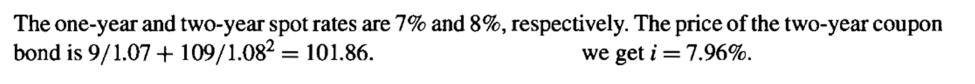
9
14.

Solution



