Process control Ziegler-Nichols PID Tuning Method

A control system with a Ziegler-Nichols PID controller is represented as shown below.

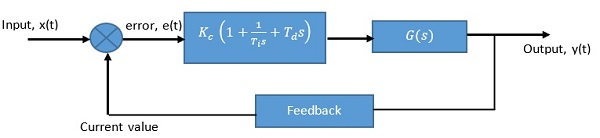
The Ziegler-Nichols rule for PID loop tuning is used to obtain approximate values for three gain parameters of the PID controller: the controller’s path gain, Kp, the derivative time constant, Td and integrator time constant, Ti. From the feedback transfer function of the system, the gain margin, Ku and the period of oscillation, Tu at the system stability limits are measured and used for tuning the PID parameters. The goal of Ziegler-Nichols PID tuning is to achieve good disturbance rejection.

In the MATLAB Code attached, the plant transfer function, G(s) is first generated from the inputs entered by the user (numerator and denominator of the transfer function). The plant transfer function is used to obtain the closed loop margins (Ku and Tu). The margins are used to calculate the critical path gain (Kc), integrator time (Ti) and the derivative time (Td) to be used for the Ziegler-Nichols PID tuning. For a classical Ziegler-Nichols controller, the values are calculated as: K_c=0.6 ×K_u,; T_i=0.5 × T_u; T_d=0.125 ×T _u

The Ziegler-Nichols PID controller is then obtained as: W _c=K_c (1+1/(T_i s)+T _d s). The compensated closed loop response is obtained by combining the Ziegler-Nichols controller in series with the plant in a unity feedback system as CLTF=feedback(series(G,W_c ),1)

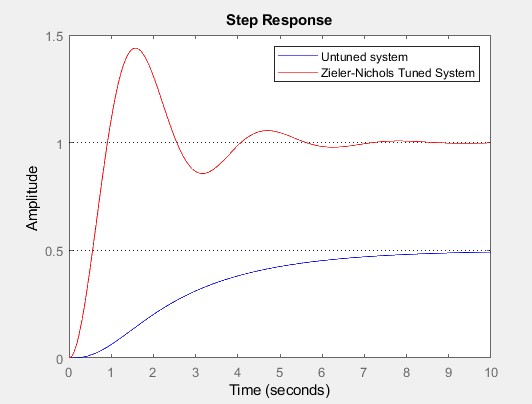
As an example, the step response of the uncompensated and compensated (controlled) systems for a third-order system transfer function, G=1/(s³+4s²+6s+1) is shown in the figure below:

                    {`
    %% To run the code, write the function name into the command window
    % For Example:
    %.........Ziegler_NicholsPID
    %............and press enter

    %% Inputs to the Ziegler Nichols PID Tuner
    % num : Numerator(starting from highest order of coefficients)in
    % form of []
    % den : Denomerator(starting from highest order of coefficients)in
    % form of []

    function ZN =Ziegler_NicholsPID()
    num=input("Enter the numerator of the open-loop system transfer function, num : ");
    den=input("Enter the denominator of the open-loop system transfer function, den : ");
    G=CreatePlant(num,den) %Plant transfer function
    G1=feedback(G,1);
    [Kcr,Pm,Wcg,Wcm]=margin(G1); %Finding margins of the uncompensated system
    Tcr=2*pi/Wcg; %Finding the time from the gain margin frequency.
    Kc=0.6*Kcr; %Critical gain
    Ti=0.5*Tcr; %Reset time (minutes)
    Td=0.125*Tcr; %Derivative time (minutes)

    %Creating Ziegler-Nichols PIDController transfer function
    Wc=ZieglerNicholsPIDController( Kc,Ti,Td )

    %Closed loop system function with Z-N controller in series with the
    %plant
    CLTF=feedback(series(G1,Wc),1)
    % Wp : Plant transfer function
    % Wc : Ziegler-Nichols PIDController transfer function
    % CLTF : Closed Loop transfer function (H=1, Unity feedback).
    t=0:0.01:10;
    figure (1)
    step(G1,t, 'b')
    hold on
    step(CLTF,t, 'r')
    hold off
    legend ("Untuned system","Zieler-Nichols Tuned System")
    end

    %% Creating the plant to control
    %CreatePlant will create the open loop plant's transfer function with the
    %num and denomitor values entered
    function [ Plant ] = CreatePlant( num,den )
    syms s;
    Plant=tf(num,den);
    end

    %% ZieglerNicholasPIDController function to generate the PID controller transfer function
    function Wc  = ZieglerNicholsPIDController( Kc,Ti,Td )
    %Parameters
    % Kc : Critical gain
    % Ti : Reset time (minutes)
    % Td : Derivative time (minutes)
    % Wc : Ziegler-Nichols PID controller in Laplace
    s=tf('s');
    Wc=Kc*(1+(1/(Ti*s))+Td*s);
    end`}