Polynomials Assignment Help

Polynomials Assignment Help

Introduction to the Polynomials

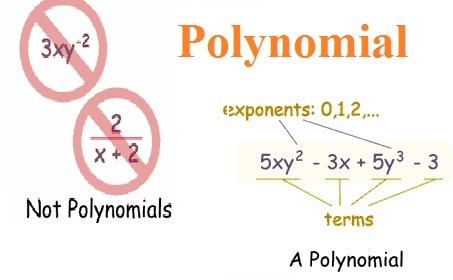
A polynomial consists of two or more terms. For example, x + y, y2 x2 and x2 + 3 x + 5 y2 are all polynomials. A polynomial is an expression consisting of variables and coefficients, that involves only the operations of addition, subtraction, multiplication and non-negative integer exponents.

Polynomial Definition

A polynomial in a single indeterminate can be written in the form.

a_nxⁿ + a_n-1x^n-1 + ... + a2x² + a1x + a₀,

---

Polynomials Assignment Help By Online Tutoring and Guided Sessions from AssignmentHelp.Net

---

Where a₀,...a_n are numbers, or more generally elements of a ring and x is a symbol which is called an indeterminate or, for historical reasons, a variable. The symbol x does not represent any value, although the usual (commutative, distributive) laws valid for arithmetic operations also apply to it.

This can be expressed more concisely by using summation notation:

Polynomial Equation:

A polynomial equation, also called algebraic equation, is an equation of the form.

a_nxⁿ + a_n-1x^n-1 + ... + a₂x² + a₁x + a₀=0

For example,

3x² + 4x - 5 = 0

is a polynomial equation.

Adding Polynomials

To add polynomials, you must clear the parenthesis, combine and add the like terms. In some cases you will need to remember the order of operations. Remember, when adding and subtracting like parts, the variable never changes.

Here are a couple of examples:

(5x + 7y) + (2x - 1y)

= 5x + 7y + 2x - 1y ----- (Clear the parenthesis)

=5x + 2x + 7y - 1y ----- (Combine the like terms)

= 7x + 6y --- (Add like terms)