Physics 2125 Experiment 7 ballistic pendulum

Objective:

The objective of this lab is to measure the initial velocity of a projectile in two independent ways. The first way is to treat it as though it is a projectile moving according to the kinematic equation. The second way is to apply the conservation of linear momentum and energy to a ballistic pendulum.

Equipment:

1. Ballistic Pendulum
2. Meter Stick
3. Plain Paper
4. Tape
5. Triple Beam Balance

Theory and Equations:

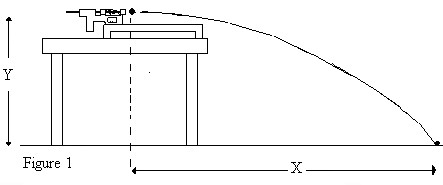
If the projectile is fired horizontally with an initial velocity V_o, it will follow the parabolic path shown in figure 1.The horizontal range x and vertical displacement y of the projectile are:

x = vt (1)

y = 1/2 gt² (2)

Eliminating the value of t from (1) and (2) we get:

V₀=x√(g/2y) (3)

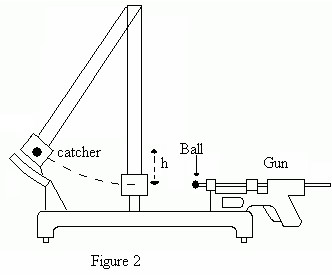
The initial velocity V_o of the projectile can also be determined by using the ballistic pendulum (Figure 2). It consists of a spring gun that fires a metallic ball of mass m. This ball is caught by a catcher at the end of a pendulum of mass M. The collision between the ball and pendulum is perfectly inelastic. As a result, the combination (m + M) swings upward until it stops at the highest point by a ratchet. 

From conservation of momentum,

mV_o = (m + M) V₁ (4)

where V₁ is the common velocity of pendulum – ball just after collision. If the combination rises through a height h, then from conservation of mechanical energy we have:

(1/2) (m + M) V₁² = ( m + M ) g h (5)

By combining (4) and (5) we determine the velocity V_o to be:

V₀ = (1+ M/m) √2gh (6)

Therefore, we can find the speed V_o of the projectile in two different ways using equation (3) and (6) and compare the results.

Procedures:

Projectile Motion

1. Move the pendulum out of the path of the ball and secure the ballistic pendulum to the table.
2. Place the ball in the shaft in the cocking position and measure the height Y from the bottom of the ball to the ground.
3. Fire the gun a few times and get an approximate position of where it strikes the ground, and then tape a piece of paper and center it around where the ball lands.
4. Shoot the ball at least five times and record the horizontal positions of each mark left on the paper.

Ballistic Pendulum

1. Remove the pendulum from the apparatus and measure its mass M and that of the ball m.
2. Reinstall the pendulum and record the distance between the base of the apparatus and the center of mass (CM) of the pendulum.
3. Place the ball in the shaft and cock the gun until the shaft is locked in position. Fire the gun and after the ball comes to rest on the curved rack, record the vertical distance between the base of the apparatus and the center of mass of the pendulum.
4. Repeat Steps 1-3 five times and record the results.

Data Table and Calculation:

Part 1 Projectile Motion

Vertical distance Y __0.828 m___

Velocity V_o of projectile from ( 3 )  _4.22 m/s_____

Part 2 Ballistic pendulum

Mass M of pendulum __0.3825 kg_

Mass m of ball ___0.0646 kg__

Velocity V_o of projectile from ( 6 ) ___3.76 m/s_____

Percent difference between the two values of V_{o ___}_11.5%____

Calculations

1. Calculate the average value for the range X of the projectile as well as its average deviation.

Average range X = (168.8+173.9+175.2+172.8+176.1)/5 = 173.6 cm = 1.736 m

Average deviation = (3.8+0.3+1.6+0.8+2.5)/5 = 1.8 cm

2. Using equation ( 3 ), calculate the initial velocity V_o of the projectile.

V_o = 1.736 m x sqrt[9.8/(2 x 0.828)] = 4.22 m/s

3. Calculate the average value for the vertical distance h the pendulum-ball system has risen after the collision. This is the difference between the height of CM at its highest point and that at its lowest point.

Average h = (1.5+1.7+1.5+1.3+1.4)/5 = 1.5 cm = 0.015 m

4. Using equation (6), calculate the initial velocity V_o of the projectile.

V_o = (1 + 382.8g/64.6g) x sqrt(2 x 9.8 x 0.015) = 3.76 m/s

5. Calculate the percent difference between the two values of V_o .

% Difference= |1^st value – 2^nd value| / [(1^st value + 2^nd value)/2] x 100%

% Difference = |4.22 – 3.76| / [(4.22 + 3.76)/2] x 100% = 11.5%

Pre Lab Questions:

1. Derive equation ( 3 ) and show that the path of the projectile is parabolic.

1. If the speed of a particle is doubled, by what factor is its momentum changed?

By what factor is its kinetic energy changed?

p = mv => if speed is doubled, momentum is doubled.

KE = ½ mv² => if speed is double, kinetic energy is quadrupled.

1. One person is standing perfectly still, and then takes a step forward. Is linear momentum conserved? Explain.

Before the step the person’s momentum was zero (no velocity), but afterward that person has some momentum. Therefore, linear momentum is not conserved. This is because the system (which is this person) is not an isolated system. The external force on the system is friction, which helps the person move forward.

1. A bullet of mass 12 grams is fired into a large block of mass 1.5 kg suspended from light vertical wires. The bullet imbeds in the block and the whole system rises 10 cm. Find the velocity of the bullet just before collision.

1. Define a perfectly inelastic collision. Give two examples of such a collision.

A perfectly inelastic collision is one in which the colliding particles stick together after the collision. In an inelastic collision, only momentum is conserved, while kinetic energy is not. Example 1: two cue balls moving toward each other with velocities opposite in direction, after the collision they have the same velocity. Example 2: An arrow is shot at a stationary apple, after the collision the arrow penetrates the apple and they moves with the same velocity.

Post Lab Questions:

• Using the value for V_o calculated from the ballistic pendulum, calculate the fractional loss in the kinetic energy during the collision.

According to the conservation of mechanical energy of the system after the collision, we have equation (5): (1/2) (m + M) V₁² = (m + M) g h 

Therefore, ∆KE = KE_f - KE_i

= ½(m + M)V₁² – ½ m(V_o)²

= (m + M) g h – ½ m(V_o)²

= (0.0646kg + 0.3828kg) x 9.8m/s² x 0.015m – ½ 0.0646kg(3.76m/s)²

= – 0.305 J (the negative sign implies the loss)

KE_i = ½ m(V_o)² = 0.457 J

Fractional loss = |∆KE |/ KE_i = 67%

• To what has this loss of energy been converted into?

This loss of energy may be converted into heat and sound.

• Derive Equation ( 6 ).

• Explain why it would have been incorrect to equate the initial kinetic energy of the ball to the final potential energy of the system.

While it is correct that the final potential energy of the pendulum-ball system is equal to the kinetic energy of this system just after the collision (due to conservation of mechanical energy after the collision). This is a perfectly inelastic collision, and consequently this kinetic energy of the pendulum-ball system after the collision is not the initial kinetic energy of the ball. In a perfectly inelastic collision, kinetic energy is not conserved.

Conclusion:

It was a bit difficult to accurately measure the x and y values in Part 1, but despite human error the percent difference between the two methods of calculating V_o was fairly low. To get an even closer approximation, we could have doubled the number of tests (from 5 to 10). One of the most important deductions from this experiment is the fact that in an inelastic collision, the kinetic energy of the system is not conserved, only the momentum is conserved.