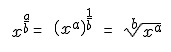Negative And Fractional Exponents Assignment Help

Introduction to Negative and Fractional Exponents:

Negative Exponent: Negative exponents are a type of the exponential forms. The exponents are also in simpler words the 'power' to which expressions are raised to. Like a2 is 'a' multiplied with itself for 2 times. A number raised to a negative fractional exponent has been defined to be the reciprocal of that number with a positive fractional exponent. When exponents are negative exponents, it means that they are placed in the denominator of a fraction. a^(-2) is nothing but 1/a²

For Example: [12]4 = 1[12]4=24

Laws of negative exponent are as follows:

x ^{- n} = 1/xⁿ

Properties - Multiplying Negative Exponent:

Multiplying Two Negative Exponent Form of Number:

(a^-m) and (a^-n)

(a^-m) * (a^-n) = a^{(-m + (-n))}

Fractional Exponents

The exponents are nothing but a short way of representing a number and are basically the number of times the base is multiplied by itself. In some cases the operator ^ is also used to represent an exponent. A fractional exponent means the power that we raise a number to be a fraction.

Let us take x = 4

now, raise both sides to the power 12

x12 = 412

x12 = 2

Now, here x is called as base and 12 is called as fractional exponent.

Fractional exponent can be used instead of using the radical sign().

Following are the steps for solving the fractional exponents:

Step 1: Write the given equation and we have to take the fractional exponent term one side and the constant term one side

Step 2) Raise both sides to the power of reciprocal fractional exponent.

Step 3) Apply the fractional exponents rules and simplify.

Fractional law of Exponent: