MATH221 Business Mathematics II

Group Project

Part 1:

For the function

1. Find the equations of the two tangent lines at the points x = 0 and x = 1, respectively.
2. Find the intersection point of the two tangent lines, if any.

Solution:

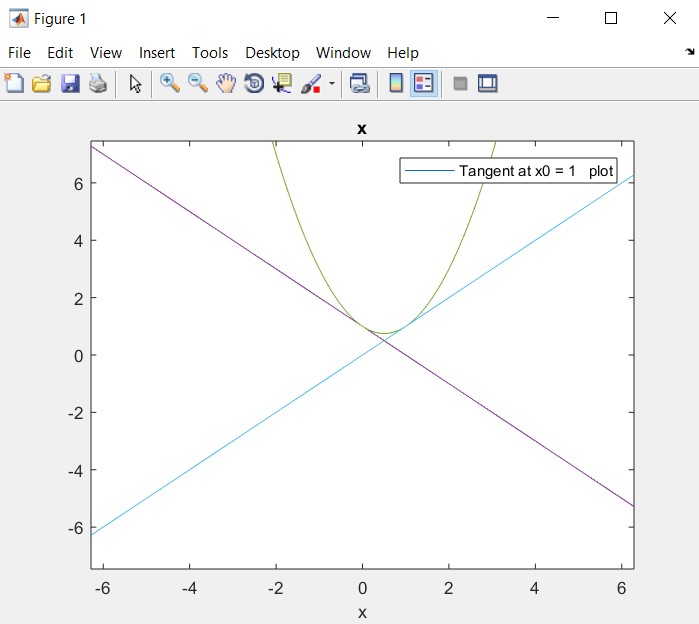
To simulate the function f(x) in MATLAB following program is executed to plot and determine the tangent.

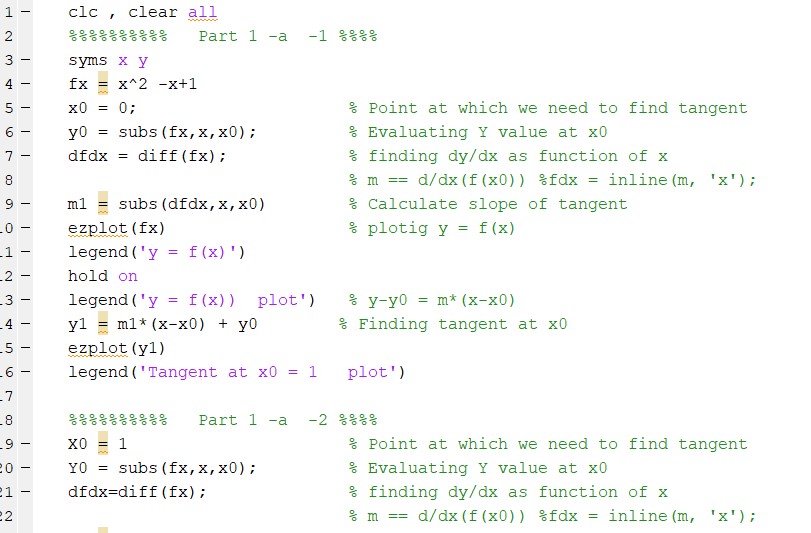
a)

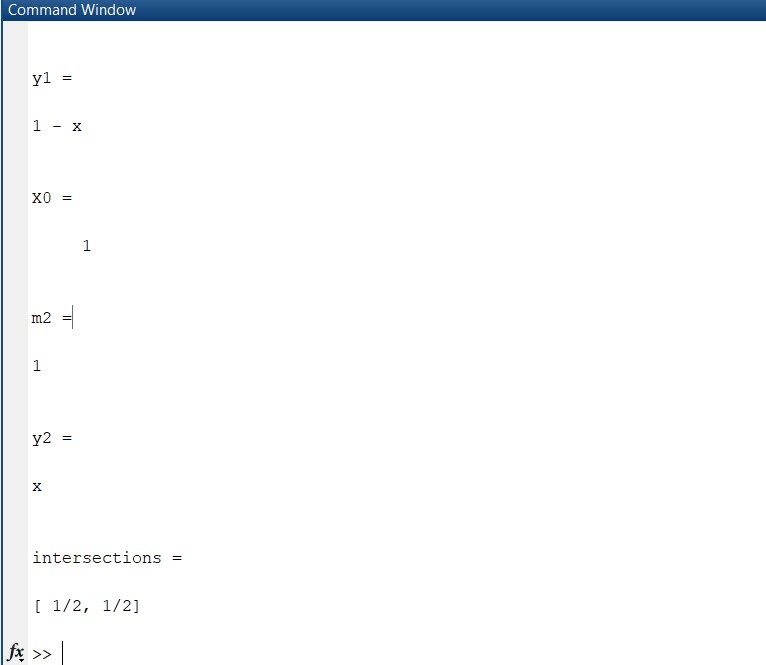
The equation of tangent line is,

y = 1 – x, for x = 0,

y = x, for x = 1

1. b) The intersection point of the two tangent lines is ( ½ , ½)

Part 2:

Consider the following demand, supply and total cost functions:

Demand function:

Supply function:

1. Determine the price and quantity at the equilibrium.
2. Calculate the consumer surplus.
3. Calculate the producer surplus.

Solution:

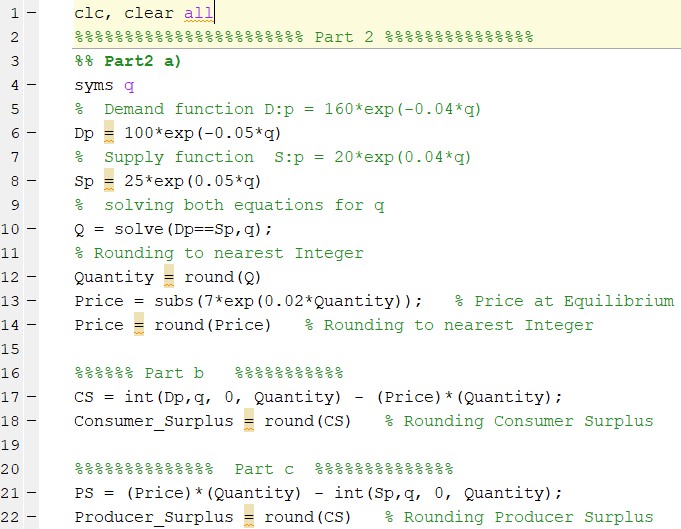
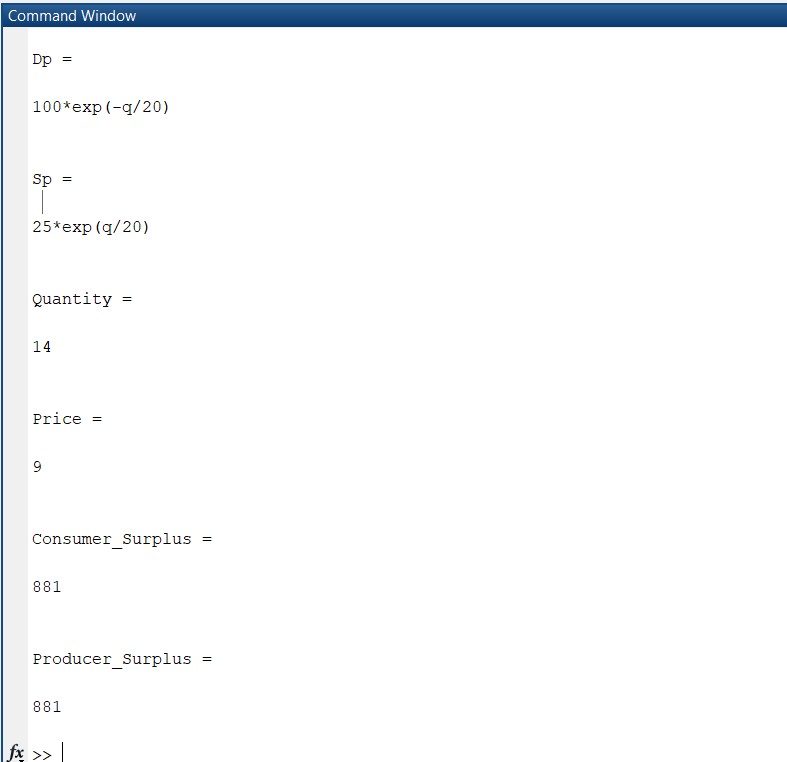
1. Determine the price and quantity at the equilibrium.

at equilibrium Demand function = Supply function.

Price is 9 units and quantity is 14 units.

1. Calculate the consumer surplus.

We have to find the area under demand curve to get Consumer Surplus for this we need to integrate Demand curev w r t Quantity from q = 0 to Equilibrium

Quantity and then subtract area (Price)x(Quantity) at equilibrium

The consumer surplus is 881.

1. Calculate the producer surplus.

We have to find the area under demand curve to get Producer Surplus for this we need to integrate Supply curve w r t Quantity from q = 0 to Equilibrium

Quantity and then subtract it from area (Price)x(Quantity) at equilibrium

The Producer surplus is 881.

Part 3

If the function is subject to the constrain

1. Use Lagrangian multipliers method to find the critical points of the function .
2. Plot the function in the 3-D graph in MATLAB.
3. Using Matlab function “fmincon”, find the maximum and minimum of the function .

Solution:

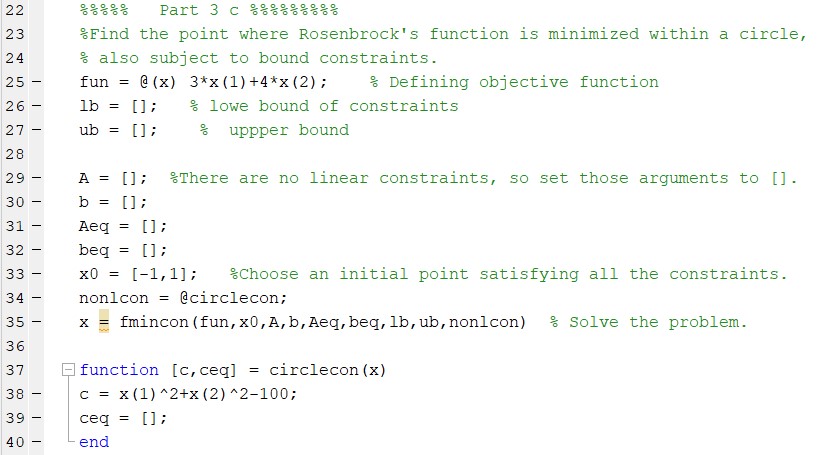
1. Use Lagrangian multipliers method to find the critical points of the function .

The critical point is -3 for the function.

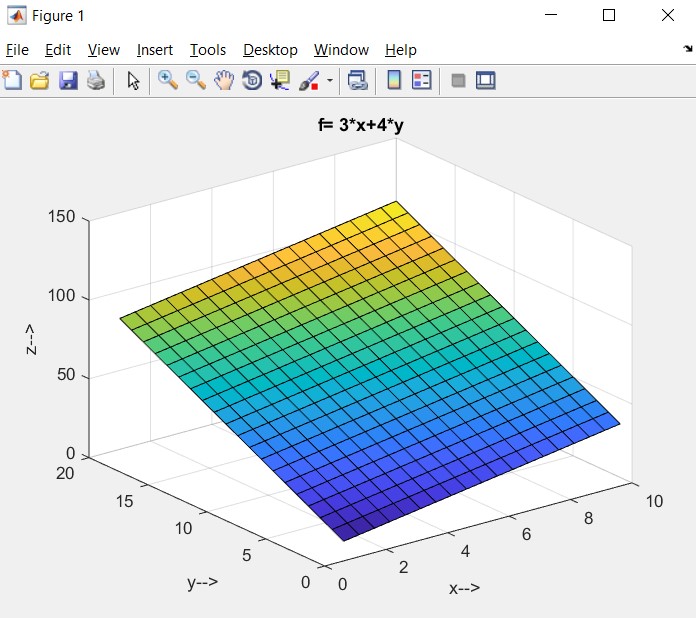
1. Plot the function in the 3-D graph in MATLAB.
   
2. Using Matlab function “fmincon”, find the maximum and minimum of the function .’
   

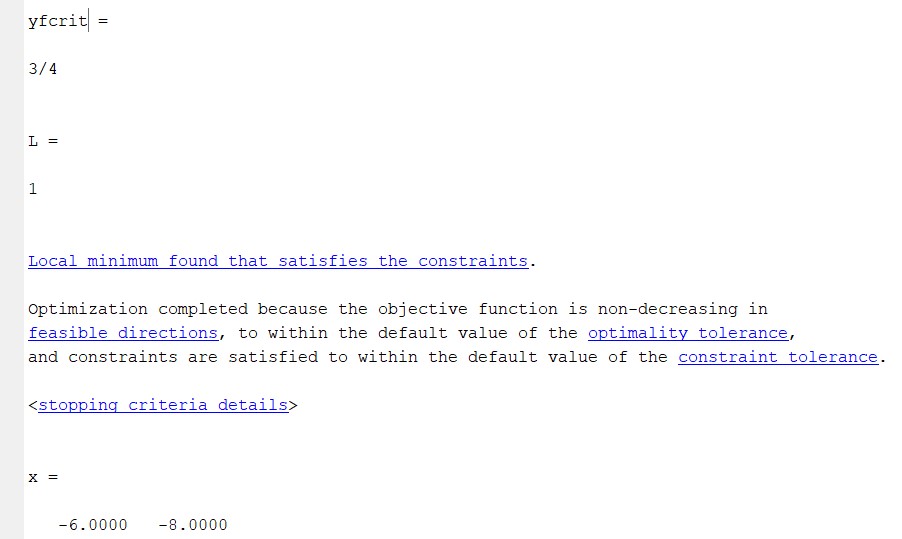
The maximum is -6.0 and minimum is -8.0 of the function.

Part 4

Suppose that a restaurant has certain fixed costs per month of $5000. The fixed costs could be interpreted as rent, insurance etc. The marginal cost function of the restaurant is given by:

dc/dq = [0.8 (0.5q² - 25q ) + 0.4]

wherec is the total cost in dollars of producing q units of good per week.

1. Find the cost of producing units, units and units per week.
2. What do you notice? Explain your results.

Solution:

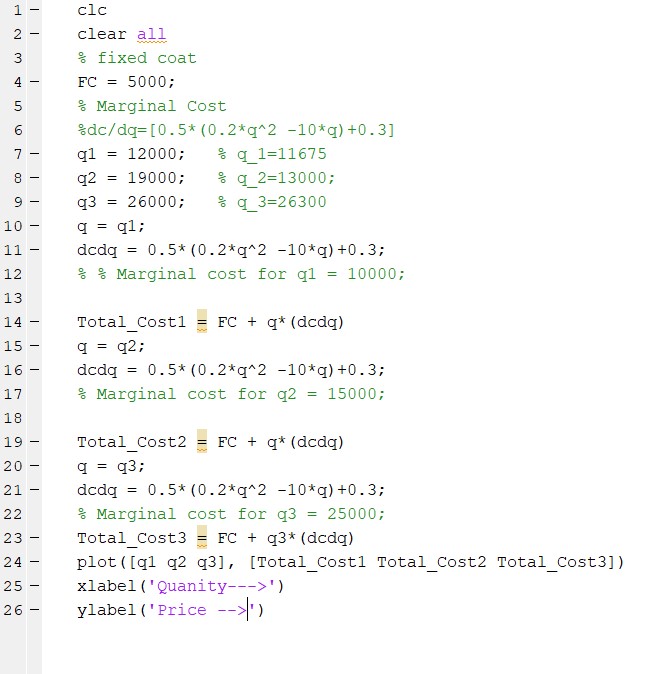
1. Find the cost of producing units, units and units per week.

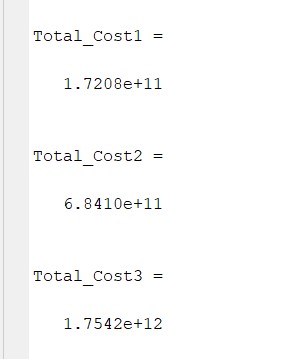
The total cost of producing q₁ is 1.7208 x 10¹¹, q₂ is 6.8410 x 10¹¹ and q₃ is 1.7542 x 10¹¹

1. What do you notice? Explain your results.

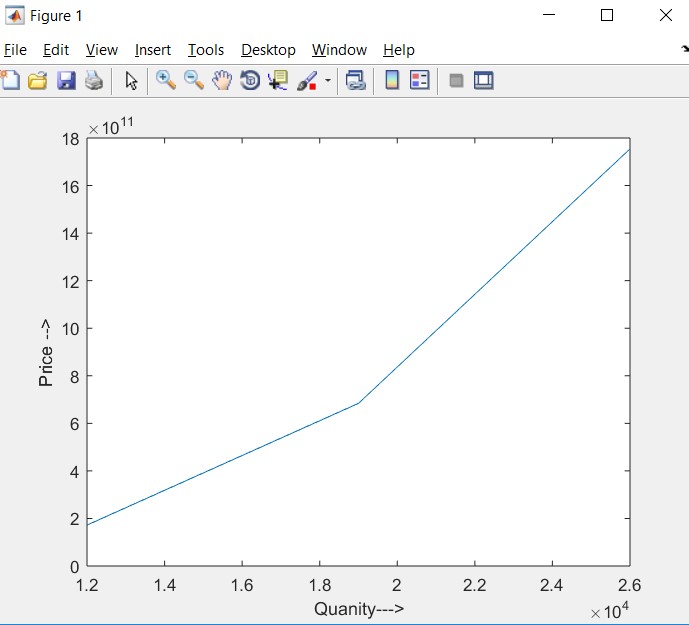
Total cost is increasing with the increase in the quantity. As it is observed from the graph of the function plotted between price and quantity.